Caution

You're reading an old version of this documentation. If you want up-to-date information, please have a look at 0.9.1.

librosa.griffinlim_cqt

librosa.griffinlim_cqt(C, n_iter=32, sr=22050, hop_length=512, fmin=None, bins_per_octave=12, tuning=0.0, filter_scale=1, norm=1, sparsity=0.01, window='hann', scale=True, pad_mode='reflect', res_type='kaiser_fast', dtype=None, length=None, momentum=0.99, init='random', random_state=None)

Approximate constant-Q magnitude spectrogram inversion using the “fast” Griffin-Lim algorithm.

Given the magnitude of a constant-Q spectrogram (C), the algorithm randomly initializes phase estimates, and then alternates forward- and inverse-CQT operations. 1

This implementation is based on the (fast) Griffin-Lim method for Short-time Fourier Transforms, 2 but adapted for use with constant-Q spectrograms.

1

D. W. Griffin and J. S. Lim, “Signal estimation from modified short-time Fourier transform,” IEEE Trans. ASSP, vol.32, no.2, pp.236–243, Apr. 1984.

2

Perraudin, N., Balazs, P., & Søndergaard, P. L. “A fast Griffin-Lim algorithm,” IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (pp. 1-4), Oct. 2013.

Parameters

Cnp.ndarray [shape=(n_bins, n_frames)]

The constant-Q magnitude spectrogram

n_iterint > 0

The number of iterations to run

srnumber > 0

Audio sampling rate

hop_lengthint > 0

The hop length of the CQT

fminnumber > 0

Minimum frequency for the CQT.

If not provided, it defaults to C1.

bins_per_octaveint > 0

Number of bins per octave

tuningfloat

Tuning deviation from A440, in fractions of a bin

filter_scalefloat > 0

Filter scale factor. Small values (<1) use shorter windows for improved time resolution.

norm{inf, -inf, 0, float > 0}

Type of norm to use for basis function normalization. See librosa.util.normalize.

sparsityfloat in [0, 1)

Sparsify the CQT basis by discarding up to sparsity fraction of the energy in each basis.

Set sparsity=0 to disable sparsification.

windowstr, tuple, or function

Window specification for the basis filters. See filters.get_window for details.

scalebool

If True, scale the CQT response by square-root the length of each channel’s filter. This is analogous to norm='ortho' in FFT.

If False, do not scale the CQT. This is analogous to norm=None in FFT.

pad_modestring

Padding mode for centered frame analysis.

See also: librosa.stft and numpy.pad.

res_typestring

The resampling mode for recursive downsampling.

By default, CQT uses an adaptive mode selection to trade accuracy at high frequencies for efficiency at low frequencies.

Griffin-Lim uses the efficient (fast) resampling mode by default.

See librosa.resample for a list of available options.

dtypenumeric type

Real numeric type for y. Default is inferred to match the precision of the input CQT.

lengthint > 0, optional

If provided, the output y is zero-padded or clipped to exactly length samples.

momentumfloat > 0

The momentum parameter for fast Griffin-Lim. Setting this to 0 recovers the original Griffin-Lim method. Values near 1 can lead to faster convergence, but above 1 may not converge.

initNone or ‘random’ [default]

If ‘random’ (the default), then phase values are initialized randomly according to random_state. This is recommended when the input C is a magnitude spectrogram with no initial phase estimates.

If None, then the phase is initialized from C. This is useful when an initial guess for phase can be provided, or when you want to resume Griffin-Lim from a previous output.

random_stateNone, int, or np.random.RandomState

If int, random_state is the seed used by the random number generator for phase initialization.

If np.random.RandomState instance, the random number generator itself.

If None, defaults to the current np.random object.

Returns

ynp.ndarray [shape=(n,)]

time-domain signal reconstructed from C

See also

cqt

icqt

griffinlim

filters.get_window

resample

Examples

A basis CQT inverse example

>>> y, sr = librosa.load(librosa.ex('trumpet', hq=True), sr=None)
>>> # Get the CQT magnitude, 7 octaves at 36 bins per octave
>>> C = np.abs(librosa.cqt(y=y, sr=sr, bins_per_octave=36, n_bins=7*36))
>>> # Invert using Griffin-Lim
>>> y_inv = librosa.griffinlim_cqt(C, sr=sr, bins_per_octave=36)
>>> # And invert without estimating phase
>>> y_icqt = librosa.icqt(C, sr=sr, bins_per_octave=36)

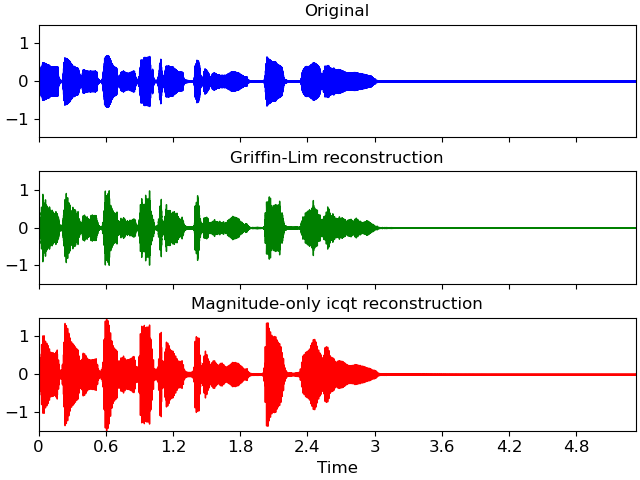
Wave-plot the results

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(nrows=3, sharex=True, sharey=True)
>>> librosa.display.waveshow(y, sr=sr, color='b', ax=ax[0])
>>> ax[0].set(title='Original', xlabel=None)
>>> ax[0].label_outer()
>>> librosa.display.waveshow(y_inv, sr=sr, color='g', ax=ax[1])
>>> ax[1].set(title='Griffin-Lim reconstruction', xlabel=None)
>>> ax[1].label_outer()
>>> librosa.display.waveshow(y_icqt, sr=sr, color='r', ax=ax[2])
>>> ax[2].set(title='Magnitude-only icqt reconstruction')