Caution

You're reading an old version of this documentation. If you want up-to-date information, please have a look at 0.9.1.

librosa.reassigned_spectrogram

librosa.reassigned_spectrogram(y, sr=22050, S=None, n_fft=2048, hop_length=None, win_length=None, window='hann', center=True, reassign_frequencies=True, reassign_times=True, ref_power=1e-06, fill_nan=False, clip=True, dtype=None, pad_mode='reflect')[source]

Time-frequency reassigned spectrogram.

The reassignment vectors are calculated using equations 5.20 and 5.23 in 1:

t_reassigned = t + np.real(S_th/S_h)
omega_reassigned = omega - np.imag(S_dh/S_h)

where S_h is the complex STFT calculated using the original window, S_dh is the complex STFT calculated using the derivative of the original window, and S_th is the complex STFT calculated using the original window multiplied by the time offset from the window center. See 2 for additional algorithms, and 3 and 4 for history and discussion of the method.

1

Flandrin, P., Auger, F., & Chassande-Mottin, E. (2002). Time-Frequency reassignment: From principles to algorithms. In Applications in Time-Frequency Signal Processing (Vol. 10, pp. 179-204). CRC Press.

2

Fulop, S. A., & Fitz, K. (2006). Algorithms for computing the time-corrected instantaneous frequency (reassigned) spectrogram, with applications. The Journal of the Acoustical Society of America, 119(1), 360. doi:10.1121/1.2133000

3

Auger, F., Flandrin, P., Lin, Y.-T., McLaughlin, S., Meignen, S., Oberlin, T., & Wu, H.-T. (2013). Time-Frequency Reassignment and Synchrosqueezing: An Overview. IEEE Signal Processing Magazine, 30(6), 32-41. doi:10.1109/MSP.2013.2265316

4

Hainsworth, S., Macleod, M. (2003). Time-frequency reassignment: a review and analysis. Tech. Rep. CUED/FINFENG/TR.459, Cambridge University Engineering Department

Parameters
ynp.ndarray [shape=(n,)], real-valued

audio time series

srnumber > 0 [scalar]

sampling rate of y

Snp.ndarray [shape=(d, t)] or None

(optional) complex STFT calculated using the other arguments provided to reassigned_spectrogram

n_fftint > 0 [scalar]

FFT window size. Defaults to 2048.

hop_lengthint > 0 [scalar]

hop length, number samples between subsequent frames. If not supplied, defaults to win_length // 4.

win_lengthint > 0, <= n_fft

Window length. Defaults to n_fft. See stft for details.

windowstring, tuple, number, function, or np.ndarray [shape=(n_fft,)]

See stft for details.

centerboolean

  • If True (default), the signal y is padded so that frame S[:, t] is centered at y[t * hop_length]. See Notes for recommended usage in this function.

  • If False, then S[:, t] begins at y[t * hop_length].

reassign_frequenciesboolean

  • If True (default), the returned frequencies will be instantaneous frequency estimates.

  • If False, the returned frequencies will be a read-only view of the STFT bin frequencies for all frames.

reassign_timesboolean

  • If True (default), the returned times will be corrected (reassigned) time estimates for each bin.

  • If False, the returned times will be a read-only view of the STFT frame times for all bins.

ref_powerfloat >= 0 or callable

Minimum power threshold for estimating time-frequency reassignments. Any bin with np.abs(S[f, t])**2 < ref_power will be returned as np.nan in both frequency and time, unless fill_nan is True. If 0 is provided, then only bins with zero power will be returned as np.nan (unless fill_nan=True).

fill_nanboolean

  • If False (default), the frequency and time reassignments for bins below the power threshold provided in ref_power will be returned as np.nan.

  • If True, the frequency and time reassignments for these bins will be returned as the bin center frequencies and frame times.

clipboolean

  • If True (default), estimated frequencies outside the range [0, 0.5 * sr] or times outside the range [0, len(y) / sr] will be clipped to those ranges.

  • If False, estimated frequencies and times beyond the bounds of the spectrogram may be returned.

dtypenumeric type

Complex numeric type for STFT calculation. Default is inferred to match the precision of the input signal.

pad_modestring

If center=True, the padding mode to use at the edges of the signal. By default, STFT uses reflection padding.

Returns
freqs, times, magsnp.ndarray [shape=(1 + n_fft/2, t), dtype=real]
Instantaneous frequencies:

freqs[f, t] is the frequency for bin f, frame t. If reassign_frequencies=False, this will instead be a read-only array of the same shape containing the bin center frequencies for all frames.

Reassigned times:

times[f, t] is the time for bin f, frame t. If reassign_times=False, this will instead be a read-only array of the same shape containing the frame times for all bins.

Magnitudes from short-time Fourier transform:

mags[f, t] is the magnitude for bin f, frame t.

Warns
RuntimeWarning

Frequency or time estimates with zero support will produce a divide-by-zero warning, and will be returned as np.nan unless fill_nan=True.

See also

stft

Short-time Fourier Transform

Notes

It is recommended to use center=False with this function rather than the librosa default True. Unlike stft, reassigned times are not aligned to the left or center of each frame, so padding the signal does not affect the meaning of the reassigned times. However, reassignment assumes that the energy in each FFT bin is associated with exactly one signal component and impulse event. The default center=True with reflection padding can thus invalidate the reassigned estimates in the half-reflected frames at the beginning and end of the signal.

If reassign_times is False, the frame times that are returned will be aligned to the left or center of the frame, depending on the value of center. In this case, if center is True, then pad_mode="wrap" is recommended for valid estimation of the instantaneous frequencies in the boundary frames.

Examples

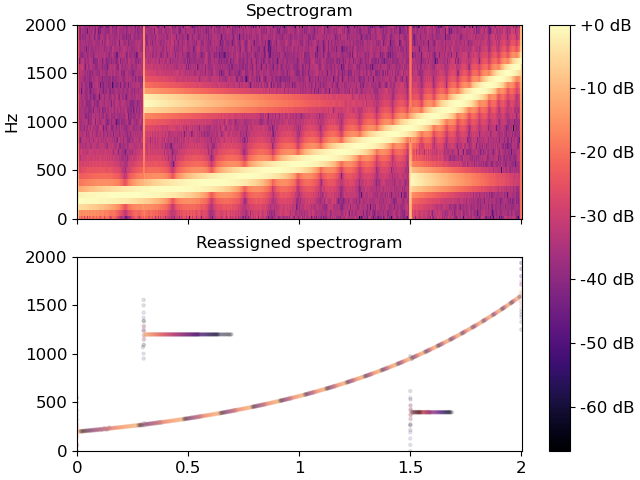
>>> import matplotlib.pyplot as plt
>>> amin = 1e-10
>>> n_fft = 64
>>> sr = 4000
>>> y = 1e-3 * librosa.clicks(times=[0.3], sr=sr, click_duration=1.0,
...                           click_freq=1200.0, length=8000) +\
...     1e-3 * librosa.clicks(times=[1.5], sr=sr, click_duration=0.5,
...                           click_freq=400.0, length=8000) +\
...     1e-3 * librosa.chirp(200, 1600, sr=sr, duration=2.0) +\
...     1e-6 * np.random.randn(2*sr)
>>> freqs, times, mags = librosa.reassigned_spectrogram(y=y, sr=sr,
...                                                     n_fft=n_fft)
>>> mags_db = librosa.power_to_db(mags, ref=np.max)

>>> fig, ax = plt.subplots(nrows=2, sharex=True, sharey=True)
>>> img = librosa.display.specshow(mags_db, x_axis="s", y_axis="linear", sr=sr,
...                          hop_length=n_fft//4, ax=ax[0])
>>> ax[0].set(title="Spectrogram", xlabel=None)
>>> ax[0].label_outer()
>>> ax[1].scatter(times, freqs, c=mags_db, cmap="magma", alpha=0.1, s=5)
>>> ax[1].set_title("Reassigned spectrogram")
>>> fig.colorbar(img, ax=ax, format="%+2.f dB")
../_images/librosa-reassigned_spectrogram-1.png