Caution

You're reading the documentation for a development version. For the latest released version, please have a look at 0.9.1.

librosa.filters.constant_q

librosa.filters.constant_q(*, sr, fmin=None, n_bins=84, bins_per_octave=12, window='hann', filter_scale=1, pad_fft=True, norm=1, dtype=<class 'numpy.complex64'>, gamma=0, **kwargs)

Construct a constant-Q basis.

This function constructs a filter bank similar to Morlet wavelets, where complex exponentials are windowed to different lengths such that the number of cycles remains fixed for all frequencies.

By default, a Hann window (rather than the Gaussian window of Morlet wavelets) is used, but this can be controlled by the window parameter.

Frequencies are spaced geometrically, increasing by a factor of (2**(1./bins_per_octave)) at each successive band.

Warning

This function is deprecated as of v0.9 and will be removed in 1.0. See librosa.filters.wavelet.

Parameters

srnumber > 0 [scalar]

Audio sampling rate

fminfloat > 0 [scalar]

Minimum frequency bin. Defaults to C1 ~= 32.70

n_binsint > 0 [scalar]

Number of frequencies. Defaults to 7 octaves (84 bins).

bins_per_octaveint > 0 [scalar]

Number of bins per octave

windowstring, tuple, number, or function

Windowing function to apply to filters.

filter_scalefloat > 0 [scalar]

Scale of filter windows. Small values (<1) use shorter windows for higher temporal resolution.

pad_fftboolean

Center-pad all filters up to the nearest integral power of 2.

By default, padding is done with zeros, but this can be overridden by setting the mode= field in kwargs.

norm{inf, -inf, 0, float > 0}

Type of norm to use for basis function normalization. See librosa.util.normalize

gammanumber >= 0

Bandwidth offset for variable-Q transforms. gamma=0 produces a constant-Q filterbank.

dtypenp.dtype

The data type of the output basis. By default, uses 64-bit (single precision) complex floating point.

**kwargsadditional keyword arguments

Arguments to np.pad() when pad==True.

Returns

filtersnp.ndarray, len(filters) == n_bins

filters[i] is ith time-domain CQT basis filter

lengthsnp.ndarray, len(lengths) == n_bins

The (fractional) length of each filter

See also

wavelet

constant_q_lengths

librosa.cqt

librosa.vqt

librosa.util.normalize

Notes

This function caches at level 10.

Examples

Use a shorter window for each filter

>>> basis, lengths = librosa.filters.constant_q(sr=22050, filter_scale=0.5)

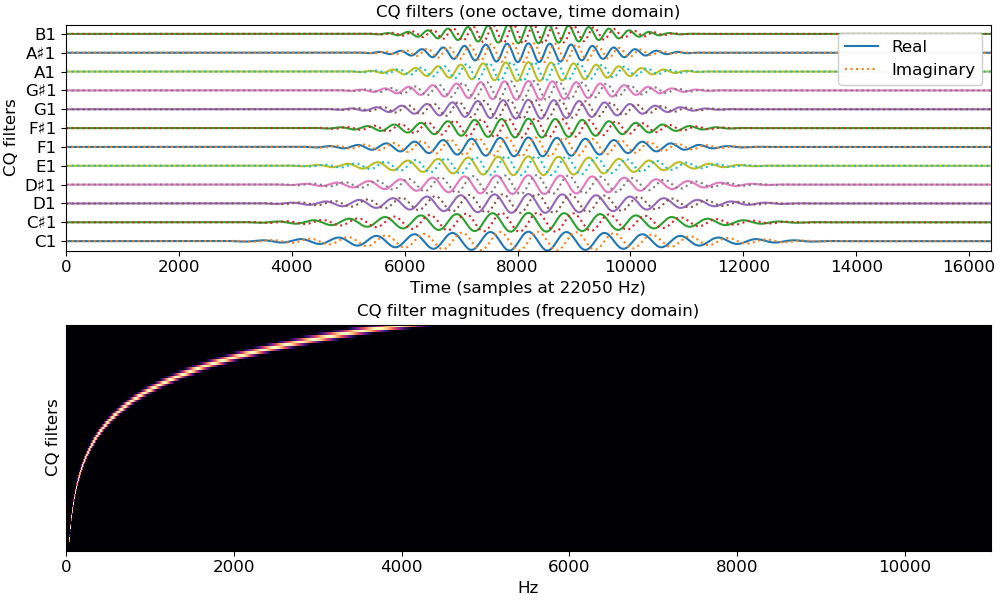
Plot one octave of filters in time and frequency

>>> import matplotlib.pyplot as plt
>>> basis, lengths = librosa.filters.constant_q(sr=22050)
>>> fig, ax = plt.subplots(nrows=2, figsize=(10, 6))
>>> notes = librosa.midi_to_note(np.arange(24, 24 + len(basis)))
>>> for i, (f, n) in enumerate(zip(basis, notes[:12])):
...     f_scale = librosa.util.normalize(f) / 2
...     ax[0].plot(i + f_scale.real)
...     ax[0].plot(i + f_scale.imag, linestyle=':')
>>> ax[0].set(yticks=np.arange(len(notes[:12])), yticklabels=notes[:12],
...           ylabel='CQ filters',
...           title='CQ filters (one octave, time domain)',
...           xlabel='Time (samples at 22050 Hz)')
>>> ax[0].legend(['Real', 'Imaginary'])
>>> F = np.abs(np.fft.fftn(basis, axes=[-1]))
>>> # Keep only the positive frequencies
>>> F = F[:, :(1 + F.shape[1] // 2)]
>>> librosa.display.specshow(F, x_axis='linear', y_axis='cqt_note', ax=ax[1])
>>> ax[1].set(ylabel='CQ filters', title='CQ filter magnitudes (frequency domain)')