Caution

You're reading the documentation for a development version. For the latest released version, please have a look at 0.9.1.

librosa.stft¶

librosa.stft(y, *, n_fft=2048, hop_length=None, win_length=None, window='hann', center=True, dtype=None, pad_mode='constant')[source]¶

Short-time Fourier transform (STFT).

The STFT represents a signal in the time-frequency domain by computing discrete Fourier transforms (DFT) over short overlapping windows.

This function returns a complex-valued matrix D such that

np.abs(D[..., f, t]) is the magnitude of frequency bin f at frame t, and
np.angle(D[..., f, t]) is the phase of frequency bin f at frame t.

The integers t and f can be converted to physical units by means of the utility functions frames_to_sample and fft_frequencies.

Parameters

ynp.ndarray [shape=(…, n)], real-valued

input signal. Multi-channel is supported.

n_fftint > 0 [scalar]

length of the windowed signal after padding with zeros. The number of rows in the STFT matrix D is (1 + n_fft/2). The default value, n_fft=2048 samples, corresponds to a physical duration of 93 milliseconds at a sample rate of 22050 Hz, i.e. the default sample rate in librosa. This value is well adapted for music signals. However, in speech processing, the recommended value is 512, corresponding to 23 milliseconds at a sample rate of 22050 Hz. In any case, we recommend setting n_fft to a power of two for optimizing the speed of the fast Fourier transform (FFT) algorithm.

hop_lengthint > 0 [scalar]

number of audio samples between adjacent STFT columns.

Smaller values increase the number of columns in D without affecting the frequency resolution of the STFT.

If unspecified, defaults to win_length // 4 (see below).

win_lengthint <= n_fft [scalar]

Each frame of audio is windowed by window of length win_length and then padded with zeros to match n_fft.

Smaller values improve the temporal resolution of the STFT (i.e. the ability to discriminate impulses that are closely spaced in time) at the expense of frequency resolution (i.e. the ability to discriminate pure tones that are closely spaced in frequency). This effect is known as the time-frequency localization trade-off and needs to be adjusted according to the properties of the input signal y.

If unspecified, defaults to win_length = n_fft.

windowstring, tuple, number, function, or np.ndarray [shape=(n_fft,)]

Either:

a window specification (string, tuple, or number); see scipy.signal.get_window
a window function, such as scipy.signal.windows.hann
a vector or array of length n_fft

Defaults to a raised cosine window (‘hann’), which is adequate for most applications in audio signal processing.

centerboolean

If True, the signal y is padded so that frame D[:, t] is centered at y[t * hop_length].

If False, then D[:, t] begins at y[t * hop_length].

Defaults to True, which simplifies the alignment of D onto a time grid by means of librosa.frames_to_samples. Note, however, that center must be set to False when analyzing signals with librosa.stream.

dtypenp.dtype, optional

Complex numeric type for D. Default is inferred to match the precision of the input signal.

pad_modestring or function

If center=True, this argument is passed to np.pad for padding the edges of the signal y. By default (pad_mode="constant"), y is padded on both sides with zeros. If center=False, this argument is ignored.

Returns

Dnp.ndarray [shape=(…, 1 + n_fft/2, n_frames), dtype=dtype]: Complex-valued matrix of short-term Fourier transform coefficients.

See also

istft: Inverse STFT
reassigned_spectrogram: Time-frequency reassigned spectrogram

Notes

This function caches at level 20.

Examples

>>> y, sr = librosa.load(librosa.ex('trumpet'))
>>> S = np.abs(librosa.stft(y))
>>> S
array([[5.395e-03, 3.332e-03, ..., 9.862e-07, 1.201e-05],
       [3.244e-03, 2.690e-03, ..., 9.536e-07, 1.201e-05],
       ...,
       [7.523e-05, 3.722e-05, ..., 1.188e-04, 1.031e-03],
       [7.640e-05, 3.944e-05, ..., 5.180e-04, 1.346e-03]],
      dtype=float32)

Use left-aligned frames, instead of centered frames

>>> S_left = librosa.stft(y, center=False)

Use a shorter hop length

>>> D_short = librosa.stft(y, hop_length=64)

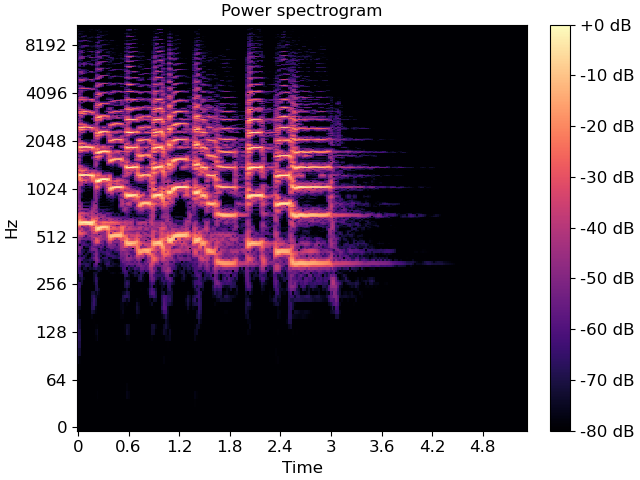
Display a spectrogram

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> img = librosa.display.specshow(librosa.amplitude_to_db(S,
...                                                        ref=np.max),
...                                y_axis='log', x_axis='time', ax=ax)
>>> ax.set_title('Power spectrogram')
>>> fig.colorbar(img, ax=ax, format="%+2.0f dB")