Caution
You're reading an old version of this documentation. If you want up-to-date information, please have a look at 0.10.2.
librosa.segment.cross_similarity
- librosa.segment.cross_similarity(data, data_ref, *, k=None, metric='euclidean', sparse=False, mode='connectivity', bandwidth=None, full=False)[source]
Compute cross-similarity from one data sequence to a reference sequence.
The output is a matrix
xsim, wherexsim[i, j]is non-zero ifdata_ref[..., i]is a k-nearest neighbor ofdata[..., j].- Parameters:
- datanp.ndarray [shape=(…, d, n)]
A feature matrix for the comparison sequence. If the data has more than two dimensions (e.g., for multi-channel inputs), the leading dimensions are flattened prior to comparison. For example, a stereo input with shape (2, d, n) is automatically reshaped to (2 * d, n).
- data_refnp.ndarray [shape=(…, d, n_ref)]
A feature matrix for the reference sequence If the data has more than two dimensions (e.g., for multi-channel inputs), the leading dimensions are flattened prior to comparison. For example, a stereo input with shape (2, d, n_ref) is automatically reshaped to (2 * d, n_ref).
- kint > 0 [scalar] or None
the number of nearest-neighbors for each sample
Default:
k = 2 * ceil(sqrt(n_ref)), ork = 2ifn_ref <= 3- metricstr
Distance metric to use for nearest-neighbor calculation.
See
sklearn.neighbors.NearestNeighborsfor details.- sparsebool [scalar]
if False, returns a dense type (ndarray) if True, returns a sparse type (scipy.sparse.csc_matrix)
- modestr, {‘connectivity’, ‘distance’, ‘affinity’}
If ‘connectivity’, a binary connectivity matrix is produced.
If ‘distance’, then a non-zero entry contains the distance between points.
If ‘affinity’, then non-zero entries are mapped to
exp( - distance(i, j) / bandwidth)wherebandwidthis as specified below.- bandwidthNone, float > 0, ndarray, or str
str options include
{'med_k_scalar', 'mean_k', 'gmean_k', 'mean_k_avg', 'gmean_k_avg', 'mean_k_avg_and_pair'}If ndarray is supplied, use ndarray as bandwidth for each i,j pair.
If using
mode='affinity', this can be used to set the bandwidth on the affinity kernel.If no value is provided or
None, default to'med_k_scalar'.If
bandwidth='med_k_scalar', bandwidth is set automatically to the median distance to the k’th nearest neighbor of eachdata[:, i].If
bandwidth='mean_k', bandwidth is estimated for each sample-pair (i, j) by taking the arithmetic mean between distances to the k-th nearest neighbor for sample i and sample j.If
bandwidth='gmean_k', bandwidth is estimated for each sample-pair (i, j) by taking the geometric mean between distances to the k-th nearest neighbor for sample i and j [1].If
bandwidth='mean_k_avg', bandwidth is estimated for each sample-pair (i, j) by taking the arithmetic mean between the average distances to the first k-th nearest neighbors for sample i and sample j. This is similar to the approach in Wang et al. (2014) [2] but does not include the distance between i and j.If
bandwidth='gmean_k_avg', bandwidth is estimated for each sample-pair (i, j) by taking the geometric mean between the average distances to the first k-th nearest neighbors for sample i and sample j.If
bandwidth='mean_k_avg_and_pair', bandwidth is estimated for each sample-pair (i, j) by taking the arithmetic mean between three terms: the average distances to the first k-th nearest neighbors for sample i and sample j respectively, as well as the distance between i and j. This is similar to the approach in Wang et al. (2014). [2]- fullbool
If using
mode ='affinity'ormode='distance', this option can be used to compute the full affinity or distance matrix as opposed a sparse matrix with only none-zero terms for the first k-neighbors of each sample. This option has no effect when usingmode='connectivity'.When using
mode='distance', settingfull=Truewill ignorekandwidth. When usingmode='affinity', settingfull=Truewill usekexclusively for bandwidth estimation, and ignorewidth.
- Returns:
- xsimnp.ndarray or scipy.sparse.csc_matrix, [shape=(n_ref, n)]
Cross-similarity matrix
See also
Notes
This function caches at level 30.
Examples
Find nearest neighbors in CQT space between two sequences
>>> hop_length = 1024 >>> y_ref, sr = librosa.load(librosa.ex('pistachio')) >>> y_comp, sr = librosa.load(librosa.ex('pistachio'), offset=10) >>> chroma_ref = librosa.feature.chroma_cqt(y=y_ref, sr=sr, hop_length=hop_length) >>> chroma_comp = librosa.feature.chroma_cqt(y=y_comp, sr=sr, hop_length=hop_length) >>> # Use time-delay embedding to get a cleaner recurrence matrix >>> x_ref = librosa.feature.stack_memory(chroma_ref, n_steps=10, delay=3) >>> x_comp = librosa.feature.stack_memory(chroma_comp, n_steps=10, delay=3) >>> xsim = librosa.segment.cross_similarity(x_comp, x_ref)
Or fix the number of nearest neighbors to 5
>>> xsim = librosa.segment.cross_similarity(x_comp, x_ref, k=5)
Use cosine similarity instead of Euclidean distance
>>> xsim = librosa.segment.cross_similarity(x_comp, x_ref, metric='cosine')
Use an affinity matrix instead of binary connectivity
>>> xsim_aff = librosa.segment.cross_similarity(x_comp, x_ref, metric='cosine', mode='affinity')
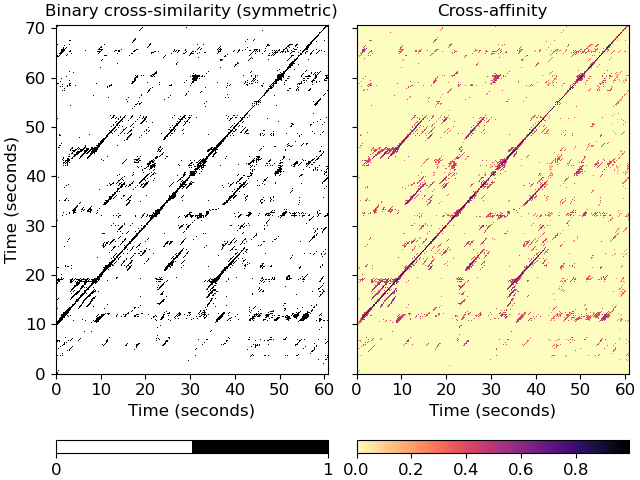
Plot the feature and recurrence matrices
>>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots(ncols=2, sharex=True, sharey=True) >>> imgsim = librosa.display.specshow(xsim, x_axis='s', y_axis='s', ... hop_length=hop_length, ax=ax[0]) >>> ax[0].set(title='Binary cross-similarity (symmetric)') >>> imgaff = librosa.display.specshow(xsim_aff, x_axis='s', y_axis='s', ... cmap='magma_r', hop_length=hop_length, ax=ax[1]) >>> ax[1].set(title='Cross-affinity') >>> ax[1].label_outer() >>> fig.colorbar(imgsim, ax=ax[0], orientation='horizontal', ticks=[0, 1]) >>> fig.colorbar(imgaff, ax=ax[1], orientation='horizontal')