Caution

You're reading an old version of this documentation. If you want up-to-date information, please have a look at 0.10.2.

librosa.util.cyclic_gradient

librosa.util.cyclic_gradient(data, *, edge_order=1, axis=-1)

Estimate the gradient of a function over a uniformly sampled, periodic domain.

This is essentially the same as np.gradient, except that edge effects are handled by wrapping the observations (i.e. assuming periodicity) rather than extrapolation.

Parameters:

datanp.ndarray

The function values observed at uniformly spaced positions on a periodic domain

edge_order{1, 2}

The order of the difference approximation used for estimating the gradient

axisint

The axis along which gradients are calculated.

Returns:

gradnp.ndarray like data

The gradient of data taken along the specified axis.

See also

numpy.gradient

Examples

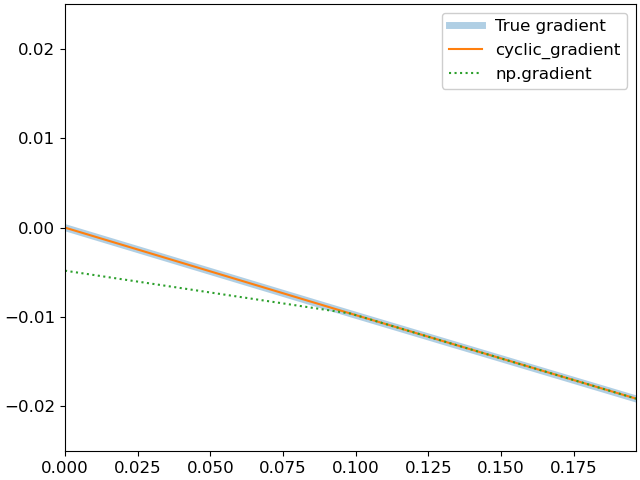
This example estimates the gradient of cosine (-sine) from 64 samples using direct (aperiodic) and periodic gradient calculation.

>>> import matplotlib.pyplot as plt
>>> x = 2 * np.pi * np.linspace(0, 1, num=64, endpoint=False)
>>> y = np.cos(x)
>>> grad = np.gradient(y)
>>> cyclic_grad = librosa.util.cyclic_gradient(y)
>>> true_grad = -np.sin(x) * 2 * np.pi / len(x)
>>> fig, ax = plt.subplots()
>>> ax.plot(x, true_grad, label='True gradient', linewidth=5,
...          alpha=0.35)
>>> ax.plot(x, cyclic_grad, label='cyclic_gradient')
>>> ax.plot(x, grad, label='np.gradient', linestyle=':')
>>> ax.legend()
>>> # Zoom into the first part of the sequence
>>> ax.set(xlim=[0, np.pi/16], ylim=[-0.025, 0.025])