Caution

You're reading the documentation for a development version. For the latest released version, please have a look at 0.10.2.

librosa.filters.semitone_filterbank

librosa.filters.semitone_filterbank(*, center_freqs=None, tuning=0.0, sample_rates=None, flayout='ba', **kwargs)

Construct a multi-rate bank of infinite-impulse response (IIR) band-pass filters at user-defined center frequencies and sample rates.

By default, these center frequencies are set equal to the 88 fundamental frequencies of the grand piano keyboard, according to a pitch tuning standard of A440, that is, note A above middle C set to 440 Hz. The center frequencies are tuned to the twelve-tone equal temperament, which means that they grow exponentially at a rate of 2**(1/12), that is, twelve notes per octave.

The A440 tuning can be changed by the user while keeping twelve-tone equal temperament. While A440 is currently the international standard in the music industry (ISO 16), some orchestras tune to A441-A445, whereas baroque musicians tune to A415.

See [1] for details.

[1]

Müller, Meinard. “Information Retrieval for Music and Motion.” Springer Verlag. 2007.

Parameters:

center_freqsnp.ndarray [shape=(n,), dtype=float]

Center frequencies of the filter kernels. Also defines the number of filters in the filterbank.

tuningfloat [scalar]

Tuning deviation from A440 as a fraction of a semitone (1/12 of an octave in equal temperament).

sample_ratesnp.ndarray [shape=(n,), dtype=float]

Sample rates of each filter in the multirate filterbank.

flayoutstring

• If ba, the standard difference equation is used for filtering with scipy.signal.filtfilt. Can be unstable for high-order filters.

• If sos, a series of second-order filters is used for filtering with scipy.signal.sosfiltfilt. Minimizes numerical precision errors for high-order filters, but is slower.

**kwargsadditional keyword arguments

Additional arguments to the private function _multirate_fb().

Returns:

filterbanklist [shape=(n,), dtype=float]

Each list entry contains the filter coefficients for a single filter.

fb_sample_ratesnp.ndarray [shape=(n,), dtype=float]

Sample rate for each filter.

See also

librosa.cqt

librosa.iirt

librosa.filters.mr_frequencies

scipy.signal.iirdesign

Examples

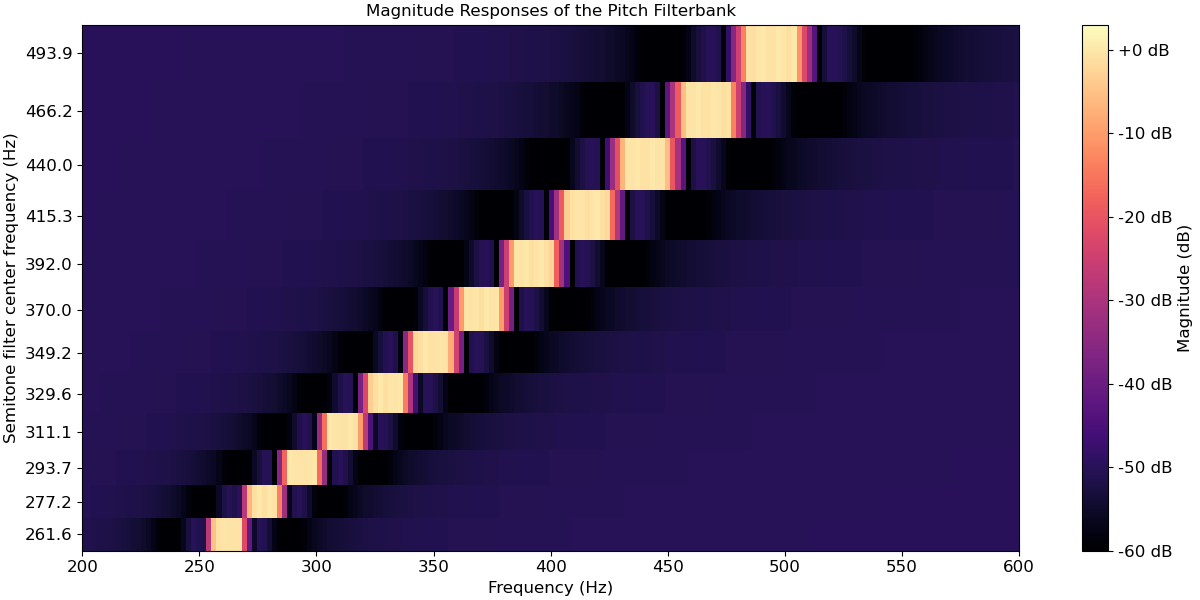
>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> import scipy.signal
>>> semitone_filterbank, sample_rates = librosa.filters.semitone_filterbank(
...     center_freqs=librosa.midi_to_hz(np.arange(60, 72)),
...     sample_rates=np.repeat(4410.0, 12),
...     flayout='sos'
...     )
>>> magnitudes = []
>>> for cur_sr, cur_filter in zip(sample_rates, semitone_filterbank):
...     w, h = scipy.signal.sosfreqz(cur_filter,fs=cur_sr, worN=1025)
...     magnitudes.append(20 * np.log10(np.abs(h)))
>>> fig, ax = plt.subplots(figsize=(12,6))
>>> img = librosa.display.specshow(
...     np.array(magnitudes),
...     x_axis="hz",
...     sr=4410,
...     y_coords=librosa.midi_to_hz(np.arange(60, 72)),
...     vmin=-60,
...     vmax=3,
...     ax=ax
...     )
>>> fig.colorbar(img, ax=ax, format="%+2.f dB", label="Magnitude (dB)")
>>> ax.set(
...     xlim=[200, 600],
...     yticks=librosa.midi_to_hz(np.arange(60, 72)),
...     title='Magnitude Responses of the Pitch Filterbank',
...     xlabel='Frequency (Hz)',
...     ylabel='Semitone filter center frequency (Hz)'
... )