Caution

You're reading an old version of this documentation. If you want up-to-date information, please have a look at 0.10.2.

librosa.griffinlim

librosa.griffinlim(S, *, n_iter=32, hop_length=None, win_length=None, n_fft=None, window='hann', center=True, dtype=None, length=None, pad_mode='constant', momentum=0.99, init='random', random_state=None)[source]

Approximate magnitude spectrogram inversion using the “fast” Griffin-Lim algorithm.

Given a short-time Fourier transform magnitude matrix (S), the algorithm randomly initializes phase estimates, and then alternates forward- and inverse-STFT operations. [1]

Note that this assumes reconstruction of a real-valued time-domain signal, and that S contains only the non-negative frequencies (as computed by stft).

The “fast” GL method [2] uses a momentum parameter to accelerate convergence.

Parameters:

Snp.ndarray [shape=(…, n_fft // 2 + 1, t), non-negative]

An array of short-time Fourier transform magnitudes as produced by stft.

n_iterint > 0

The number of iterations to run

hop_lengthNone or int > 0

The hop length of the STFT. If not provided, it will default to n_fft // 4

win_lengthNone or int > 0

The window length of the STFT. By default, it will equal n_fft

n_fftNone or int > 0

The number of samples per frame. By default, this will be inferred from the shape of S as an even number. However, if an odd frame length was used, you can explicitly set n_fft.

windowstring, tuple, number, function, or np.ndarray [shape=(n_fft,)]

A window specification as supported by stft or istft

centerboolean

If True, the STFT is assumed to use centered frames. If False, the STFT is assumed to use left-aligned frames.

dtypenp.dtype

Real numeric type for the time-domain signal. Default is inferred to match the precision of the input spectrogram.

lengthNone or int > 0

If provided, the output y is zero-padded or clipped to exactly length samples.

pad_modestring

If center=True, the padding mode to use at the edges of the signal. By default, STFT uses zero padding.

momentumnumber >= 0

The momentum parameter for fast Griffin-Lim. Setting this to 0 recovers the original Griffin-Lim method [1]. Values near 1 can lead to faster convergence, but above 1 may not converge.

initNone or ‘random’ [default]

If ‘random’ (the default), then phase values are initialized randomly according to random_state. This is recommended when the input S is a magnitude spectrogram with no initial phase estimates.

If None, then the phase is initialized from S. This is useful when an initial guess for phase can be provided, or when you want to resume Griffin-Lim from a previous output.

random_stateNone, int, np.random.RandomState, or np.random.Generator

If int, random_state is the seed used by the random number generator for phase initialization.

If np.random.RandomState or np.random.Generator instance, the random number generator itself.

If None, defaults to the np.random.default_rng() object.

Returns:

ynp.ndarray [shape=(…, n)]: time-domain signal reconstructed from S

See also

stft
istft
magphase
filters.get_window

Examples

A basic STFT inverse example

>>> y, sr = librosa.load(librosa.ex('trumpet'))
>>> # Get the magnitude spectrogram
>>> S = np.abs(librosa.stft(y))
>>> # Invert using Griffin-Lim
>>> y_inv = librosa.griffinlim(S)
>>> # Invert without estimating phase
>>> y_istft = librosa.istft(S)

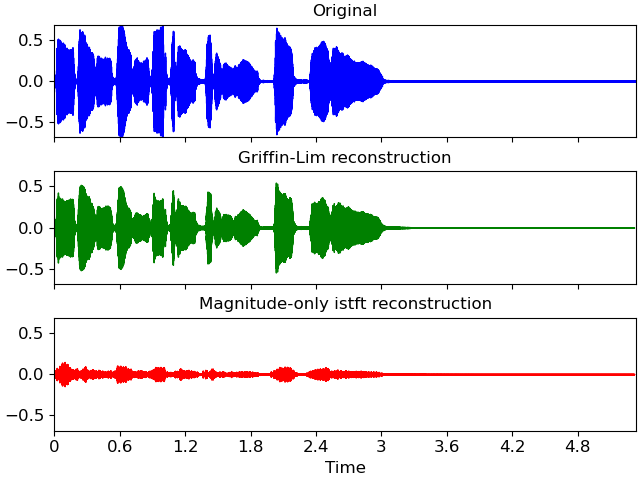
Wave-plot the results

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(nrows=3, sharex=True, sharey=True)
>>> librosa.display.waveshow(y, sr=sr, color='b', ax=ax[0])
>>> ax[0].set(title='Original', xlabel=None)
>>> ax[0].label_outer()
>>> librosa.display.waveshow(y_inv, sr=sr, color='g', ax=ax[1])
>>> ax[1].set(title='Griffin-Lim reconstruction', xlabel=None)
>>> ax[1].label_outer()
>>> librosa.display.waveshow(y_istft, sr=sr, color='r', ax=ax[2])
>>> ax[2].set_title('Magnitude-only istft reconstruction')