Caution

You're reading an old version of this documentation. If you want up-to-date information, please have a look at 0.10.2.

librosa.sequence.viterbi_discriminative

librosa.sequence.viterbi_discriminative(prob, transition, *, p_state=None, p_init=None, return_logp=False)

Viterbi decoding from discriminative state predictions.

Given a sequence of conditional state predictions prob[s, t], indicating the conditional likelihood of state s given the observation at time t, and a transition matrix transition[i, j] which encodes the conditional probability of moving from state i to state j, the Viterbi algorithm computes the most likely sequence of states from the observations.

This implementation uses the standard Viterbi decoding algorithm for observation likelihood sequences, under the assumption that P[Obs(t) | State(t) = s] is proportional to P[State(t) = s | Obs(t)] / P[State(t) = s], where the denominator is the marginal probability of state s occurring as given by p_state.

Note that because the denominator P[State(t) = s] is not explicitly calculated, the resulting probabilities (or log-probabilities) are not normalized. If using the return_logp=True option (see below), be aware that the “probabilities” may not sum to (and may exceed) 1.

Parameters:

probnp.ndarray [shape=(…, n_states, n_steps), non-negative]

prob[s, t] is the probability of state s conditional on the observation at time t. Must be non-negative and sum to 1 along each column.

transitionnp.ndarray [shape=(n_states, n_states), non-negative]

transition[i, j] is the probability of a transition from i->j. Each row must sum to 1.

p_statenp.ndarray [shape=(n_states,)]

Optional: marginal probability distribution over states, must be non-negative and sum to 1. If not provided, a uniform distribution is assumed.

p_initnp.ndarray [shape=(n_states,)]

Optional: initial state distribution. If not provided, it is assumed to be uniform.

return_logpbool

If True, return the log-likelihood of the state sequence.

Returns:

Either states or (states, logp):

statesnp.ndarray [shape=(…, n_steps,)]

The most likely state sequence. If prob contains multiple input channels, then each channel is decoded independently.

logpscalar [float] or np.ndarray

If return_logp=True, the (unnormalized) log probability of states given the observations.

See also

viterbi

Viterbi decoding from observation likelihoods

viterbi_binary

Viterbi decoding for multi-label, conditional state likelihoods

Examples

This example constructs a simple, template-based discriminative chord estimator, using CENS chroma as input features.

Note

this chord model is not accurate enough to use in practice. It is only intended to demonstrate how to use discriminative Viterbi decoding.

>>> # Create templates for major, minor, and no-chord qualities
>>> maj_template = np.array([1,0,0, 0,1,0, 0,1,0, 0,0,0])
>>> min_template = np.array([1,0,0, 1,0,0, 0,1,0, 0,0,0])
>>> N_template   = np.array([1,1,1, 1,1,1, 1,1,1, 1,1,1.]) / 4.
>>> # Generate the weighting matrix that maps chroma to labels
>>> weights = np.zeros((25, 12), dtype=float)
>>> labels = ['C:maj', 'C#:maj', 'D:maj', 'D#:maj', 'E:maj', 'F:maj',
...           'F#:maj', 'G:maj', 'G#:maj', 'A:maj', 'A#:maj', 'B:maj',
...           'C:min', 'C#:min', 'D:min', 'D#:min', 'E:min', 'F:min',
...           'F#:min', 'G:min', 'G#:min', 'A:min', 'A#:min', 'B:min',
...           'N']
>>> for c in range(12):
...     weights[c, :] = np.roll(maj_template, c) # c:maj
...     weights[c + 12, :] = np.roll(min_template, c)  # c:min
>>> weights[-1] = N_template  # the last row is the no-chord class
>>> # Make a self-loop transition matrix over 25 states
>>> trans = librosa.sequence.transition_loop(25, 0.9)

>>> # Load in audio and make features
>>> y, sr = librosa.load(librosa.ex('nutcracker'), duration=15)
>>> # Suppress percussive elements
>>> y = librosa.effects.harmonic(y, margin=4)
>>> chroma = librosa.feature.chroma_cqt(y=y, sr=sr)
>>> # Map chroma (observations) to class (state) likelihoods
>>> probs = np.exp(weights.dot(chroma))  # P[class | chroma] ~= exp(template' chroma)
>>> probs /= probs.sum(axis=0, keepdims=True)  # probabilities must sum to 1 in each column
>>> # Compute independent frame-wise estimates
>>> chords_ind = np.argmax(probs, axis=0)
>>> # And viterbi estimates
>>> chords_vit = librosa.sequence.viterbi_discriminative(probs, trans)

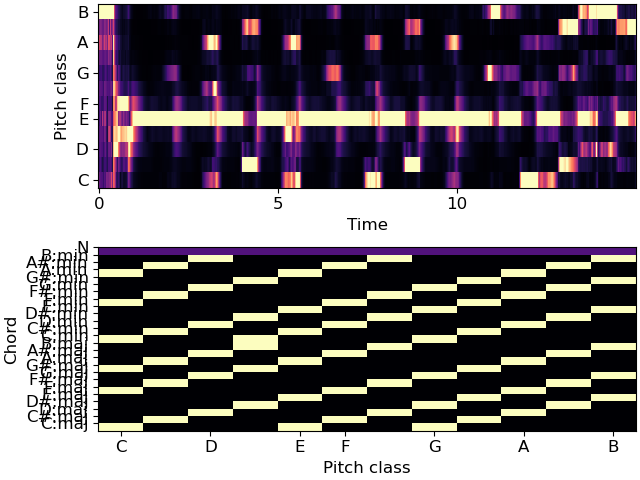
>>> # Plot the features and prediction map
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(nrows=2)
>>> librosa.display.specshow(chroma, x_axis='time', y_axis='chroma', ax=ax[0])
>>> librosa.display.specshow(weights, x_axis='chroma', ax=ax[1])
>>> ax[1].set(yticks=np.arange(25) + 0.5, yticklabels=labels, ylabel='Chord')

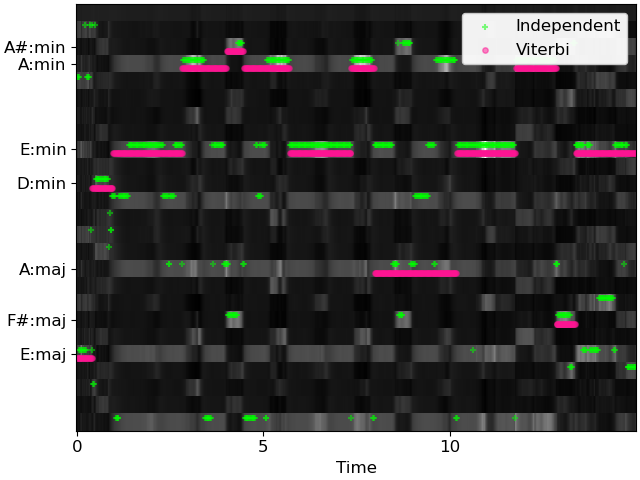
>>> # And plot the results
>>> fig, ax = plt.subplots()
>>> librosa.display.specshow(probs, x_axis='time', cmap='gray', ax=ax)
>>> times = librosa.times_like(chords_vit)
>>> ax.scatter(times, chords_ind + 0.25, color='lime', alpha=0.5, marker='+',
...            s=15, label='Independent')
>>> ax.scatter(times, chords_vit - 0.25, color='deeppink', alpha=0.5, marker='o',
...            s=15, label='Viterbi')
>>> ax.set(yticks=np.unique(chords_vit),
...        yticklabels=[labels[i] for i in np.unique(chords_vit)])
>>> ax.legend()