librosa.decompose.hpss

librosa.decompose.hpss(S, *, kernel_size=31, power=2.0, mask=False, margin=1.0)[source]

Median-filtering harmonic percussive source separation (HPSS).

If margin = 1.0, decomposes an input spectrogram S = H + P where H contains the harmonic components, and P contains the percussive components.

If margin > 1.0, decomposes an input spectrogram S = H + P + R where R contains residual components not included in H or P.

This implementation is based upon the algorithm described by [1] and [2].

Parameters:

Snp.ndarray [shape=(…, d, n)]

input spectrogram. May be real (magnitude) or complex. Multi-channel is supported.

kernel_sizeint or tuple (kernel_harmonic, kernel_percussive)

kernel size(s) for the median filters.

If scalar, the same size is used for both harmonic and percussive.
If tuple, the first value specifies the width of the harmonic filter, and the second value specifies the width of the percussive filter.

powerfloat > 0 [scalar]

Exponent for the Wiener filter when constructing soft mask matrices.

maskbool

Return the masking matrices instead of components.

Masking matrices contain non-negative real values that can be used to measure the assignment of energy from S into harmonic or percussive components.

Components can be recovered by multiplying S * mask_H or S * mask_P.

marginfloat or tuple (margin_harmonic, margin_percussive)

margin size(s) for the masks (as described in [2])

If scalar, the same size is used for both harmonic and percussive.
If tuple, the first value specifies the margin of the harmonic mask, and the second value specifies the margin of the percussive mask.

Returns:

harmonicnp.ndarray [shape=(…, d, n)]: harmonic component (or mask)
percussivenp.ndarray [shape=(…, d, n)]: percussive component (or mask)

See also

librosa.util.softmask

Notes

This function caches at level 30.

Examples

Separate into harmonic and percussive

>>> y, sr = librosa.load(librosa.ex('choice'), duration=5)
>>> D = librosa.stft(y)
>>> H, P = librosa.decompose.hpss(D)

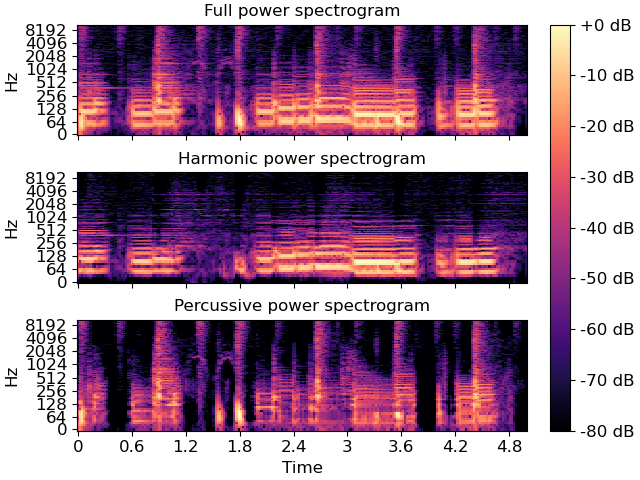
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(nrows=3, sharex=True, sharey=True)
>>> img = librosa.display.specshow(librosa.amplitude_to_db(np.abs(D),
...                                                        ref=np.max),
...                          y_axis='log', x_axis='time', ax=ax[0])
>>> ax[0].set(title='Full power spectrogram')
>>> ax[0].label_outer()
>>> librosa.display.specshow(librosa.amplitude_to_db(np.abs(H),
...                                                  ref=np.max(np.abs(D))),
...                          y_axis='log', x_axis='time', ax=ax[1])
>>> ax[1].set(title='Harmonic power spectrogram')
>>> ax[1].label_outer()
>>> librosa.display.specshow(librosa.amplitude_to_db(np.abs(P),
...                                                  ref=np.max(np.abs(D))),
...                          y_axis='log', x_axis='time', ax=ax[2])
>>> ax[2].set(title='Percussive power spectrogram')
>>> fig.colorbar(img, ax=ax, format='%+2.0f dB')

Or with a narrower horizontal filter

>>> H, P = librosa.decompose.hpss(D, kernel_size=(13, 31))

Just get harmonic/percussive masks, not the spectra

>>> mask_H, mask_P = librosa.decompose.hpss(D, mask=True)
>>> mask_H
array([[1.853e-03, 1.701e-04, ..., 9.922e-01, 1.000e+00],
       [2.316e-03, 2.127e-04, ..., 9.989e-01, 1.000e+00],
       ...,
       [8.195e-05, 6.939e-05, ..., 3.105e-04, 4.231e-04],
       [3.159e-05, 4.156e-05, ..., 6.216e-04, 6.188e-04]],
      dtype=float32)
>>> mask_P
array([[9.981e-01, 9.998e-01, ..., 7.759e-03, 3.201e-05],
       [9.977e-01, 9.998e-01, ..., 1.122e-03, 4.451e-06],
       ...,
       [9.999e-01, 9.999e-01, ..., 9.997e-01, 9.996e-01],
       [1.000e+00, 1.000e+00, ..., 9.994e-01, 9.994e-01]],
      dtype=float32)

Separate into harmonic/percussive/residual components by using a margin > 1.0

>>> H, P = librosa.decompose.hpss(D, margin=3.0)
>>> R = D - (H+P)
>>> y_harm = librosa.istft(H)
>>> y_perc = librosa.istft(P)
>>> y_resi = librosa.istft(R)

Get a more isolated percussive component by widening its margin

>>> H, P = librosa.decompose.hpss(D, margin=(1.0,5.0))