librosa.pcen

librosa.pcen(S, *, sr=22050, hop_length=512, gain=0.98, bias=2, power=0.5, time_constant=0.4, eps=1e-06, b=None, max_size=1, ref=None, axis=-1, max_axis=None, zi=None, return_zf=False)

Per-channel energy normalization (PCEN)

This function normalizes a time-frequency representation S by performing automatic gain control, followed by nonlinear compression [1]

P[f, t] = (S / (eps + M[f, t])**gain + bias)**power - bias**power

IMPORTANT: the default values of eps, gain, bias, and power match the original publication, in which S is a 40-band mel-frequency spectrogram with 25 ms windowing, 10 ms frame shift, and raw audio values in the interval [-2**31; 2**31-1[. If you use these default values, we recommend to make sure that the raw audio is properly scaled to this interval, and not to [-1, 1[ as is most often the case.

The matrix M is the result of applying a low-pass, temporal IIR filter to S:

M[f, t] = (1 - b) * M[f, t - 1] + b * S[f, t]

If b is not provided, it is calculated as:

b = (sqrt(1 + 4* T**2) - 1) / (2 * T**2)

where T = time_constant * sr / hop_length. [2]

This normalization is designed to suppress background noise and emphasize foreground signals, and can be used as an alternative to decibel scaling (amplitude_to_db).

This implementation also supports smoothing across frequency bins by specifying max_size > 1. If this option is used, the filtered spectrogram M is computed as:

M[f, t] = (1 - b) * M[f, t - 1] + b * R[f, t]

where R has been max-filtered along the frequency axis, similar to the SuperFlux algorithm implemented in onset.onset_strength:

R[f, t] = max(S[f - max_size//2: f + max_size//2, t])

This can be used to perform automatic gain control on signals that cross or span multiple frequency bans, which may be desirable for spectrograms with high frequency resolution.

[1]

Wang, Y., Getreuer, P., Hughes, T., Lyon, R. F., & Saurous, R. A. (2017, March). Trainable frontend for robust and far-field keyword spotting. In Acoustics, Speech and Signal Processing (ICASSP), 2017 IEEE International Conference on (pp. 5670-5674). IEEE.

[2]

Lostanlen, V., Salamon, J., McFee, B., Cartwright, M., Farnsworth, A., Kelling, S., and Bello, J. P. Per-Channel Energy Normalization: Why and How. IEEE Signal Processing Letters, 26(1), 39-43.

Parameters:

Snp.ndarray (non-negative)

The input (magnitude) spectrogram

srnumber > 0 [scalar]

The audio sampling rate

hop_lengthint > 0 [scalar]

The hop length of S, expressed in samples

gainnumber >= 0 [scalar]

The gain factor. Typical values should be slightly less than 1.

biasnumber >= 0 [scalar]

The bias point of the nonlinear compression (default: 2)

powernumber >= 0 [scalar]

The compression exponent. Typical values should be between 0 and 0.5. Smaller values of power result in stronger compression. At the limit power=0, polynomial compression becomes logarithmic.

time_constantnumber > 0 [scalar]

The time constant for IIR filtering, measured in seconds.

epsnumber > 0 [scalar]

A small constant used to ensure numerical stability of the filter.

bnumber in [0, 1] [scalar]

The filter coefficient for the low-pass filter. If not provided, it will be inferred from time_constant.

max_sizeint > 0 [scalar]

The width of the max filter applied to the frequency axis. If left as 1, no filtering is performed.

refNone or np.ndarray (shape=S.shape)

An optional pre-computed reference spectrum (R in the above). If not provided it will be computed from S.

axisint [scalar]

The (time) axis of the input spectrogram.

max_axisNone or int [scalar]

The frequency axis of the input spectrogram. If None, and S is two-dimensional, it will be inferred as the opposite from axis. If S is not two-dimensional, and max_size > 1, an error will be raised.

zinp.ndarray

The initial filter delay values.

This may be the zf (final delay values) of a previous call to pcen, or computed by scipy.signal.lfilter_zi.

return_zfbool

If True, return the final filter delay values along with the PCEN output P. This is primarily useful in streaming contexts, where the final state of one block of processing should be used to initialize the next block.

If False (default) only the PCEN values P are returned.

Returns:

Pnp.ndarray, non-negative [shape=(n, m)]

The per-channel energy normalized version of S.

zfnp.ndarray (optional)

The final filter delay values. Only returned if return_zf=True.

See also

amplitude_to_db

librosa.onset.onset_strength

Examples

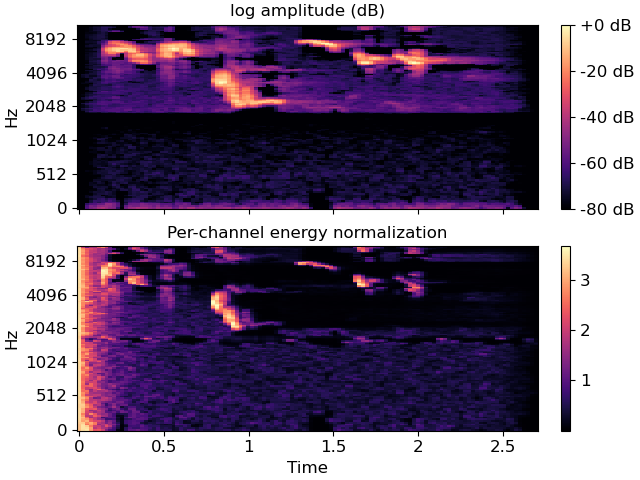
Compare PCEN to log amplitude (dB) scaling on Mel spectra

>>> import matplotlib.pyplot as plt
>>> y, sr = librosa.load(librosa.ex('robin'))

>>> # We recommend scaling y to the range [-2**31, 2**31[ before applying
>>> # PCEN's default parameters. Furthermore, we use power=1 to get a
>>> # magnitude spectrum instead of a power spectrum.
>>> S = librosa.feature.melspectrogram(y=y, sr=sr, power=1)
>>> log_S = librosa.amplitude_to_db(S, ref=np.max)
>>> pcen_S = librosa.pcen(S * (2**31))
>>> fig, ax = plt.subplots(nrows=2, sharex=True, sharey=True)
>>> img = librosa.display.specshow(log_S, x_axis='time', y_axis='mel', ax=ax[0])
>>> ax[0].set(title='log amplitude (dB)', xlabel=None)
>>> ax[0].label_outer()
>>> imgpcen = librosa.display.specshow(pcen_S, x_axis='time', y_axis='mel', ax=ax[1])
>>> ax[1].set(title='Per-channel energy normalization')
>>> fig.colorbar(img, ax=ax[0], format="%+2.0f dB")
>>> fig.colorbar(imgpcen, ax=ax[1])

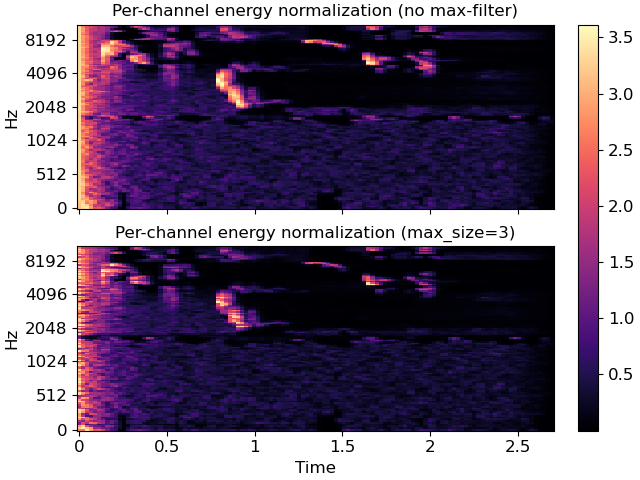
Compare PCEN with and without max-filtering

>>> pcen_max = librosa.pcen(S * (2**31), max_size=3)
>>> fig, ax = plt.subplots(nrows=2, sharex=True, sharey=True)
>>> librosa.display.specshow(pcen_S, x_axis='time', y_axis='mel', ax=ax[0])
>>> ax[0].set(title='Per-channel energy normalization (no max-filter)')
>>> ax[0].label_outer()
>>> img = librosa.display.specshow(pcen_max, x_axis='time', y_axis='mel', ax=ax[1])
>>> ax[1].set(title='Per-channel energy normalization (max_size=3)')
>>> fig.colorbar(img, ax=ax)