librosa.segment.recurrence_to_lag

librosa.segment.recurrence_to_lag(rec, *, pad=True, axis=-1)

Convert a recurrence matrix into a lag matrix.

lag[i, j] == rec[i+j, j]

This transformation turns diagonal structures in the recurrence matrix into horizontal structures in the lag matrix. These horizontal structures can be used to infer changes in the repetition structure of a piece, e.g., the beginning of a new section as done in [1].

[1]

Serra, J., Müller, M., Grosche, P., & Arcos, J. L. (2014). Unsupervised music structure annotation by time series structure features and segment similarity. IEEE Transactions on Multimedia, 16(5), 1229-1240.

Parameters:

recnp.ndarray, or scipy.sparse.spmatrix [shape=(n, n)]

A (binary) recurrence matrix, as returned by recurrence_matrix

padbool

If False, lag matrix is square, which is equivalent to assuming that the signal repeats itself indefinitely.

If True, lag is padded with n zeros, which eliminates the assumption of repetition.

axisint

The axis to keep as the time axis. The alternate axis will be converted to lag coordinates.

Returns:

lagnp.ndarray

The recurrence matrix in (lag, time) (if axis=1) or (time, lag) (if axis=0) coordinates

Raises:

ParameterErrorif rec is non-square

See also

recurrence_matrix

lag_to_recurrence

util.shear

Examples

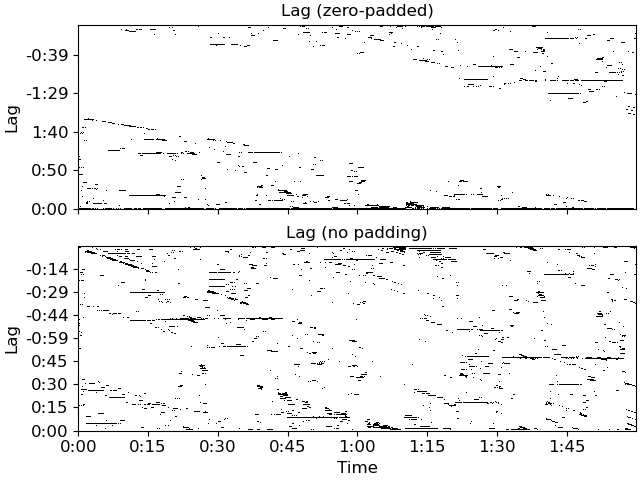
>>> y, sr = librosa.load(librosa.ex('nutcracker'))
>>> hop_length = 1024
>>> chroma = librosa.feature.chroma_cqt(y=y, sr=sr, hop_length=hop_length)
>>> chroma_stack = librosa.feature.stack_memory(chroma, n_steps=10, delay=3)
>>> recurrence = librosa.segment.recurrence_matrix(chroma_stack)
>>> lag_pad = librosa.segment.recurrence_to_lag(recurrence, pad=True)
>>> lag_nopad = librosa.segment.recurrence_to_lag(recurrence, pad=False)

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(nrows=2, sharex=True)
>>> librosa.display.specshow(lag_pad, x_axis='time', y_axis='lag',
...                          hop_length=hop_length, ax=ax[0])
>>> ax[0].set(title='Lag (zero-padded)')
>>> ax[0].label_outer()
>>> librosa.display.specshow(lag_nopad, x_axis='time', y_axis='lag',
...                          hop_length=hop_length, ax=ax[1])
>>> ax[1].set(title='Lag (no padding)')