Caution

You're reading an old version of this documentation. If you want up-to-date information, please have a look at 0.10.2.

librosa.filters.semitone_filterbank

librosa.filters.semitone_filterbank(center_freqs=None, tuning=0.0, sample_rates=None, flayout='ba', **kwargs)

Construct a multi-rate bank of infinite-impulse response (IIR) band-pass filters at user-defined center frequencies and sample rates.

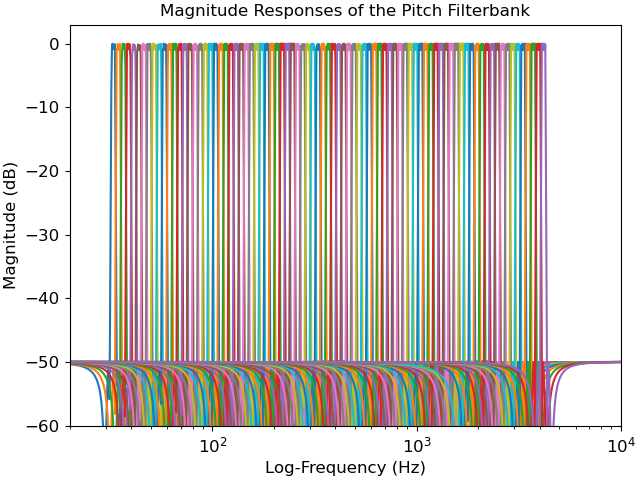
By default, these center frequencies are set equal to the 88 fundamental frequencies of the grand piano keyboard, according to a pitch tuning standard of A440, that is, note A above middle C set to 440 Hz. The center frequencies are tuned to the twelve-tone equal temperament, which means that they grow exponentially at a rate of 2**(1/12), that is, twelve notes per octave.

The A440 tuning can be changed by the user while keeping twelve-tone equal temperament. While A440 is currently the international standard in the music industry (ISO 16), some orchestras tune to A441-A445, whereas baroque musicians tune to A415.

See [1] for details.

[1]

Müller, Meinard. “Information Retrieval for Music and Motion.” Springer Verlag. 2007.

Parameters:

center_freqsnp.ndarray [shape=(n,), dtype=float]

Center frequencies of the filter kernels. Also defines the number of filters in the filterbank.

tuningfloat [scalar]

Tuning deviation from A440 as a fraction of a semitone (1/12 of an octave in equal temperament).

sample_ratesnp.ndarray [shape=(n,), dtype=float]

Sample rates of each filter in the multirate filterbank.

flayoutstring

• If ba, the standard difference equation is used for filtering with scipy.signal.filtfilt. Can be unstable for high-order filters.

• If sos, a series of second-order filters is used for filtering with scipy.signal.sosfiltfilt. Minimizes numerical precision errors for high-order filters, but is slower.

kwargsadditional keyword arguments

Additional arguments to the private function _multirate_fb().

Returns:

filterbanklist [shape=(n,), dtype=float]

Each list entry contains the filter coefficients for a single filter.

fb_sample_ratesnp.ndarray [shape=(n,), dtype=float]

Sample rate for each filter.

See also

librosa.cqt

librosa.iirt

librosa.filters.mr_frequencies

scipy.signal.iirdesign

Examples

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> import scipy.signal
>>> semitone_filterbank, sample_rates = librosa.filters.semitone_filterbank()
>>> fig, ax = plt.subplots()
>>> for cur_sr, cur_filter in zip(sample_rates, semitone_filterbank):
...    w, h = scipy.signal.freqz(cur_filter[0], cur_filter[1], worN=2000)
...    ax.semilogx((cur_sr / (2 * np.pi)) * w, 20 * np.log10(abs(h)))
>>> ax.set(xlim=[20, 10e3], ylim=[-60, 3], title='Magnitude Responses of the Pitch Filterbank',
...        xlabel='Log-Frequency (Hz)', ylabel='Magnitude (dB)')