Caution

You're reading an old version of this documentation. If you want up-to-date information, please have a look at 0.9.1.

librosa.filters.window_sumsquare

librosa.filters.window_sumsquare(window, n_frames, hop_length=512, win_length=None, n_fft=2048, dtype=<class 'numpy.float32'>, norm=None)

Compute the sum-square envelope of a window function at a given hop length.

This is used to estimate modulation effects induced by windowing observations in short-time fourier transforms.

Parameters

windowstring, tuple, number, callable, or list-like

Window specification, as in get_window

n_framesint > 0

The number of analysis frames

hop_lengthint > 0

The number of samples to advance between frames

win_length[optional]

The length of the window function. By default, this matches n_fft.

n_fftint > 0

The length of each analysis frame.

dtypenp.dtype

The data type of the output

Returns

wssnp.ndarray, shape=`(n_fft + hop_length * (n_frames - 1))`

The sum-squared envelope of the window function

Examples

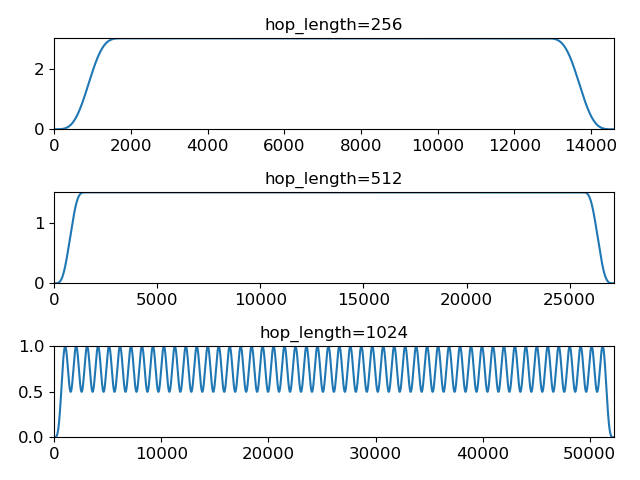
For a fixed frame length (2048), compare modulation effects for a Hann window at different hop lengths:

>>> n_frames = 50
>>> wss_256 = librosa.filters.window_sumsquare('hann', n_frames, hop_length=256)
>>> wss_512 = librosa.filters.window_sumsquare('hann', n_frames, hop_length=512)
>>> wss_1024 = librosa.filters.window_sumsquare('hann', n_frames, hop_length=1024)

>>> import matplotlib.pyplot as plt
>>> plt.figure()
>>> plt.subplot(3,1,1)
>>> plt.plot(wss_256)
>>> plt.title('hop_length=256')
>>> plt.subplot(3,1,2)
>>> plt.plot(wss_512)
>>> plt.title('hop_length=512')
>>> plt.subplot(3,1,3)
>>> plt.plot(wss_1024)
>>> plt.title('hop_length=1024')
>>> plt.tight_layout()
>>> plt.show()