Caution

You're reading an old version of this documentation. If you want up-to-date information, please have a look at 0.9.1.

librosa.sequence.dtw¶

librosa.sequence.dtw(X=None, Y=None, C=None, metric='euclidean', step_sizes_sigma=None, weights_add=None, weights_mul=None, subseq=False, backtrack=True, global_constraints=False, band_rad=0.25)[source]¶

Dynamic time warping (DTW).

This function performs a DTW and path backtracking on two sequences. We follow the nomenclature and algorithmic approach as described in [1].

1: Meinard Mueller Fundamentals of Music Processing — Audio, Analysis, Algorithms, Applications Springer Verlag, ISBN: 978-3-319-21944-8, 2015.

Parameters

Xnp.ndarray [shape=(K, N)]: audio feature matrix (e.g., chroma features)
Ynp.ndarray [shape=(K, M)]: audio feature matrix (e.g., chroma features)
Cnp.ndarray [shape=(N, M)]: Precomputed distance matrix. If supplied, X and Y must not be supplied and metric will be ignored.
metricstr: Identifier for the cost-function as documented in scipy.spatial.distance.cdist()
step_sizes_sigmanp.ndarray [shape=[n, 2]]: Specifies allowed step sizes as used by the dtw.
weights_addnp.ndarray [shape=[n, ]]: Additive weights to penalize certain step sizes.
weights_mulnp.ndarray [shape=[n, ]]: Multiplicative weights to penalize certain step sizes.
subseqbinary: Enable subsequence DTW, e.g., for retrieval tasks.
backtrackbinary: Enable backtracking in accumulated cost matrix.
global_constraintsbinary: Applies global constraints to the cost matrix C (Sakoe-Chiba band).
band_radfloat: The Sakoe-Chiba band radius (1/2 of the width) will be int(radius*min(C.shape)).

Returns

Dnp.ndarray [shape=(N,M)]: accumulated cost matrix. D[N,M] is the total alignment cost. When doing subsequence DTW, D[N,:] indicates a matching function.
wpnp.ndarray [shape=(N,2)]: Warping path with index pairs. Each row of the array contains an index pair n,m). Only returned when backtrack is True.

Raises

ParameterError

If you are doing diagonal matching and Y is shorter than X or if an incompatible combination of X, Y, and C are supplied.

If your input dimensions are incompatible.

If the cost matrix has NaN values.

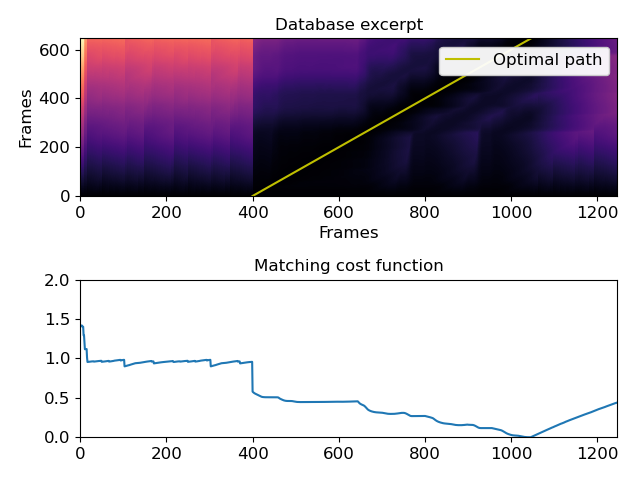
Examples

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> y, sr = librosa.load(librosa.util.example_audio_file(), offset=10, duration=15)
>>> X = librosa.feature.chroma_cens(y=y, sr=sr)
>>> noise = np.random.rand(X.shape[0], 200)
>>> Y = np.concatenate((noise, noise, X, noise), axis=1)
>>> D, wp = librosa.sequence.dtw(X, Y, subseq=True)
>>> plt.subplot(2, 1, 1)
>>> librosa.display.specshow(D, x_axis='frames', y_axis='frames')
>>> plt.title('Database excerpt')
>>> plt.plot(wp[:, 1], wp[:, 0], label='Optimal path', color='y')
>>> plt.legend()
>>> plt.subplot(2, 1, 2)
>>> plt.plot(D[-1, :] / wp.shape[0])
>>> plt.xlim([0, Y.shape[1]])
>>> plt.ylim([0, 2])
>>> plt.title('Matching cost function')
>>> plt.tight_layout()
>>> plt.show()