Caution

You're reading an old version of this documentation. If you want up-to-date information, please have a look at 0.9.1.

librosa.util.nnls

librosa.util.nnls(A, B, **kwargs)

Non-negative least squares.

Given two matrices A and B, find a non-negative matrix X that minimizes the sum squared error:

err(X) = sum_i,j ((AX)[i,j] - B[i, j])^2

Parameters

Anp.ndarray [shape=(m, n)]

The basis matrix

Bnp.ndarray [shape=(m, N)]

The target matrix.

kwargs

Additional keyword arguments to scipy.optimize.fmin_l_bfgs_b

Returns

Xnp.ndarray [shape=(n, N), non-negative]

A minimizing solution to |AX - B|^2

See also

scipy.optimize.nnls

scipy.optimize.fmin_l_bfgs_b

Examples

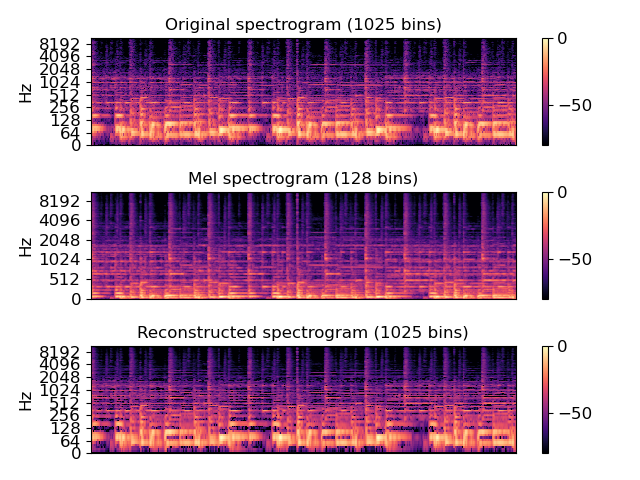
Approximate a magnitude spectrum from its mel spectrogram

>>> y, sr = librosa.load(librosa.util.example_audio_file(), offset=30, duration=10)
>>> S = np.abs(librosa.stft(y, n_fft=2048))
>>> M = librosa.feature.melspectrogram(S=S, sr=sr, power=1)
>>> mel_basis = librosa.filters.mel(sr, n_fft=2048, n_mels=M.shape[0])
>>> S_recover = librosa.util.nnls(mel_basis, M)

Plot the results

>>> import matplotlib.pyplot as plt
>>> plt.figure()
>>> plt.subplot(3,1,1)
>>> librosa.display.specshow(librosa.amplitude_to_db(S, ref=np.max), y_axis='log')
>>> plt.colorbar()
>>> plt.title('Original spectrogram (1025 bins)')
>>> plt.subplot(3,1,2)
>>> librosa.display.specshow(librosa.amplitude_to_db(M, ref=np.max),
...                          y_axis='mel')
>>> plt.title('Mel spectrogram (128 bins)')
>>> plt.colorbar()
>>> plt.subplot(3,1,3)
>>> librosa.display.specshow(librosa.amplitude_to_db(S_recover, ref=np.max),
...                          y_axis='log')
>>> plt.colorbar()
>>> plt.title('Reconstructed spectrogram (1025 bins)')
>>> plt.tight_layout()
>>> plt.show()