Caution

You're reading an old version of this documentation. If you want up-to-date information, please have a look at 0.9.1.

librosa.sequence.rqa

librosa.sequence.rqa(sim, *, gap_onset=1, gap_extend=1, knight_moves=True, backtrack=True)

Recurrence quantification analysis (RQA)

This function implements different forms of RQA as described by Serra, Serra, and Andrzejak (SSA). 1 These methods take as input a self- or cross-similarity matrix sim, and calculate the value of path alignments by dynamic programming.

Note that unlike dynamic time warping (dtw), alignment paths here are maximized, not minimized, so the input should measure similarity rather than distance.

The simplest RQA method, denoted as L (SSA equation 3) and equivalent to the method described by Eckman, Kamphorst, and Ruelle 2, accumulates the length of diagonal paths with positive values in the input:

• score[i, j] = score[i-1, j-1] + 1 if sim[i, j] > 0

• score[i, j] = 0 otherwise.

The second method, denoted as S (SSA equation 4), is similar to the first, but allows for “knight moves” (as in the chess piece) in addition to strict diagonal moves:

• score[i, j] = max(score[i-1, j-1], score[i-2, j-1], score[i-1, j-2]) + 1 if sim[i, j] > 0

• score[i, j] = 0 otherwise.

The third method, denoted as Q (SSA equations 5 and 6) extends this by allowing gaps in the alignment that incur some cost, rather than a hard reset to 0 whenever sim[i, j] == 0. Gaps are penalized by two additional parameters, gap_onset and gap_extend, which are subtracted from the value of the alignment path every time a gap is introduced or extended (respectively).

Note that setting gap_onset and gap_extend to np.inf recovers the second method, and disabling knight moves recovers the first.

1

Serrà, Joan, Xavier Serra, and Ralph G. Andrzejak. “Cross recurrence quantification for cover song identification.” New Journal of Physics 11, no. 9 (2009): 093017.

2

Eckmann, J. P., S. Oliffson Kamphorst, and D. Ruelle. “Recurrence plots of dynamical systems.” World Scientific Series on Nonlinear Science Series A 16 (1995): 441-446.

Parameters

simnp.ndarray [shape=(N, M), non-negative]

The similarity matrix to use as input.

This can either be a recurrence matrix (self-similarity) or a cross-similarity matrix between two sequences.

gap_onsetfloat > 0

Penalty for introducing a gap to an alignment sequence

gap_extendfloat > 0

Penalty for extending a gap in an alignment sequence

knight_movesbool

If True (default), allow for “knight moves” in the alignment, e.g., (n, m) => (n + 1, m + 2) or (n + 2, m + 1).

If False, only allow for diagonal moves (n, m) => (n + 1, m + 1).

backtrackbool

If True, return the alignment path.

If False, only return the score matrix.

Returns

scorenp.ndarray [shape=(N, M)]

The alignment score matrix. score[n, m] is the cumulative value of the best alignment sequence ending in frames n and m.

pathnp.ndarray [shape=(k, 2)] (optional)

If backtrack=True, path contains a list of pairs of aligned frames in the best alignment sequence.

path[i] = [n, m] indicates that row n aligns to column m.

See also

librosa.segment.recurrence_matrix

librosa.segment.cross_similarity

dtw

Examples

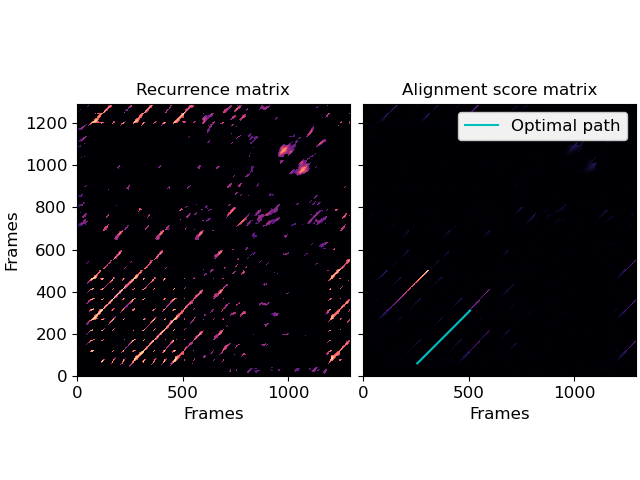
Simple diagonal path enhancement (L-mode)

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> y, sr = librosa.load(librosa.ex('nutcracker'), duration=30)
>>> chroma = librosa.feature.chroma_cqt(y=y, sr=sr)
>>> # Use time-delay embedding to reduce noise
>>> chroma_stack = librosa.feature.stack_memory(chroma, n_steps=10, delay=3)
>>> # Build recurrence, suppress self-loops within 1 second
>>> rec = librosa.segment.recurrence_matrix(chroma_stack, width=43,
...                                         mode='affinity',
...                                         metric='cosine')
>>> # using infinite cost for gaps enforces strict path continuation
>>> L_score, L_path = librosa.sequence.rqa(rec,
...                                        gap_onset=np.inf,
...                                        gap_extend=np.inf,
...                                        knight_moves=False)
>>> fig, ax = plt.subplots(ncols=2)
>>> librosa.display.specshow(rec, x_axis='frames', y_axis='frames', ax=ax[0])
>>> ax[0].set(title='Recurrence matrix')
>>> librosa.display.specshow(L_score, x_axis='frames', y_axis='frames', ax=ax[1])
>>> ax[1].set(title='Alignment score matrix')
>>> ax[1].plot(L_path[:, 1], L_path[:, 0], label='Optimal path', color='c')
>>> ax[1].legend()
>>> ax[1].label_outer()

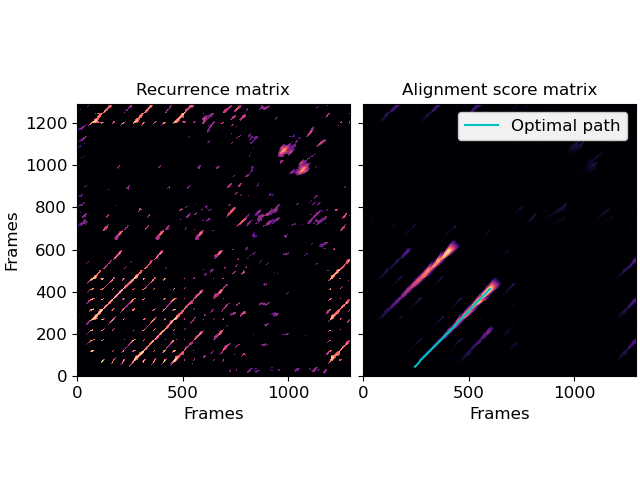
Full alignment using gaps and knight moves

>>> # New gaps cost 5, extending old gaps cost 10 for each step
>>> score, path = librosa.sequence.rqa(rec, gap_onset=5, gap_extend=10)
>>> fig, ax = plt.subplots(ncols=2, sharex=True, sharey=True)
>>> librosa.display.specshow(rec, x_axis='frames', y_axis='frames', ax=ax[0])
>>> ax[0].set(title='Recurrence matrix')
>>> librosa.display.specshow(score, x_axis='frames', y_axis='frames', ax=ax[1])
>>> ax[1].set(title='Alignment score matrix')
>>> ax[1].plot(path[:, 1], path[:, 0], label='Optimal path', color='c')
>>> ax[1].legend()
>>> ax[1].label_outer()