librosa.segment.path_enhance

librosa.segment.path_enhance(R, n, *, window='hann', max_ratio=2.0, min_ratio=None, n_filters=7, zero_mean=False, clip=True, **kwargs)

Multi-angle path enhancement for self- and cross-similarity matrices.

This function convolves multiple diagonal smoothing filters with a self-similarity (or recurrence) matrix R, and aggregates the result by an element-wise maximum.

Technically, the output is a matrix R_smooth such that:

R_smooth[i, j] = max_theta (R * filter_theta)[i, j]

where * denotes 2-dimensional convolution, and filter_theta is a smoothing filter at orientation theta.

This is intended to provide coherent temporal smoothing of self-similarity matrices when there are changes in tempo.

Smoothing filters are generated at evenly spaced orientations between min_ratio and max_ratio.

This function is inspired by the multi-angle path enhancement of 1, but differs by modeling tempo differences in the space of similarity matrices rather than re-sampling the underlying features prior to generating the self-similarity matrix.

1

Müller, Meinard and Frank Kurth. “Enhancing similarity matrices for music audio analysis.” 2006 IEEE International Conference on Acoustics Speech and Signal Processing Proceedings. Vol. 5. IEEE, 2006.

Note

if using recurrence_matrix to construct the input similarity matrix, be sure to include the main diagonal by setting self=True. Otherwise, the diagonal will be suppressed, and this is likely to produce discontinuities which will pollute the smoothing filter response.

Parameters

Rnp.ndarray

The self- or cross-similarity matrix to be smoothed. Note: sparse inputs are not supported.

If the recurrence matrix is multi-dimensional, e.g. shape=(c, n, n), then enhancement is conducted independently for each leading channel.

nint > 0

The length of the smoothing filter

windowwindow specification

The type of smoothing filter to use. See filters.get_window for more information on window specification formats.

max_ratiofloat > 0

The maximum tempo ratio to support

min_ratiofloat > 0

The minimum tempo ratio to support. If not provided, it will default to 1/max_ratio

n_filtersint >= 1

The number of different smoothing filters to use, evenly spaced between min_ratio and max_ratio.

If min_ratio = 1/max_ratio (the default), using an odd number of filters will ensure that the main diagonal (ratio=1) is included.

zero_meanbool

By default, the smoothing filters are non-negative and sum to one (i.e. are averaging filters).

If zero_mean=True, then the smoothing filters are made to sum to zero by subtracting a constant value from the non-diagonal coordinates of the filter. This is primarily useful for suppressing blocks while enhancing diagonals.

clipbool

If True, the smoothed similarity matrix will be thresholded at 0, and will not contain negative entries.

**kwargsadditional keyword arguments

Additional arguments to pass to scipy.ndimage.convolve

Returns

R_smoothnp.ndarray, shape=R.shape

The smoothed self- or cross-similarity matrix

See also

librosa.filters.diagonal_filter

recurrence_matrix

Examples

Use a 51-frame diagonal smoothing filter to enhance paths in a recurrence matrix

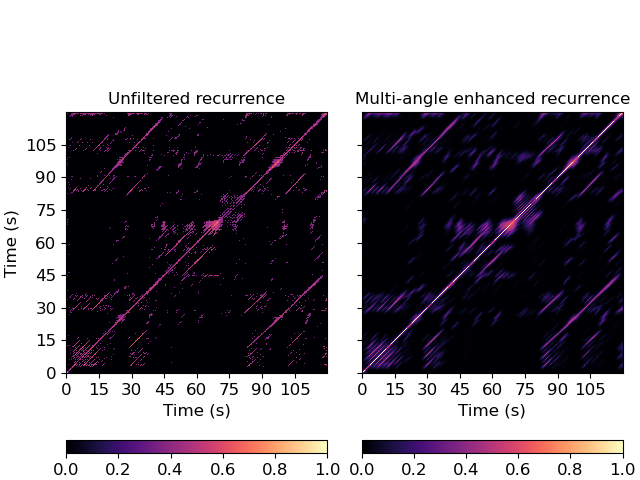
>>> y, sr = librosa.load(librosa.ex('nutcracker'))
>>> hop_length = 2048
>>> chroma = librosa.feature.chroma_cqt(y=y, sr=sr, hop_length=hop_length)
>>> chroma_stack = librosa.feature.stack_memory(chroma, n_steps=10, delay=3)
>>> rec = librosa.segment.recurrence_matrix(chroma_stack, mode='affinity', self=True)
>>> rec_smooth = librosa.segment.path_enhance(rec, 51, window='hann', n_filters=7)

Plot the recurrence matrix before and after smoothing

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(ncols=2, sharex=True, sharey=True)
>>> img = librosa.display.specshow(rec, x_axis='s', y_axis='s',
...                          hop_length=hop_length, ax=ax[0])
>>> ax[0].set(title='Unfiltered recurrence')
>>> imgpe = librosa.display.specshow(rec_smooth, x_axis='s', y_axis='s',
...                          hop_length=hop_length, ax=ax[1])
>>> ax[1].set(title='Multi-angle enhanced recurrence')
>>> ax[1].label_outer()
>>> fig.colorbar(img, ax=ax[0], orientation='horizontal')
>>> fig.colorbar(imgpe, ax=ax[1], orientation='horizontal')