Caution

You're reading the documentation for a development version. For the latest released version, please have a look at 0.10.2.

librosa.segment.cross_similarity

librosa.segment.cross_similarity(data, data_ref, *, k=None, metric='euclidean', sparse=False, mode='connectivity', bandwidth=None, full=False)

Compute cross-similarity from one data sequence to a reference sequence.

The output is a matrix xsim, where xsim[i, j] is non-zero if data_ref[..., i] is a k-nearest neighbor of data[..., j].

Parameters:

datanp.ndarray [shape=(…, d, n)]

A feature matrix for the comparison sequence. If the data has more than two dimensions (e.g., for multi-channel inputs), the leading dimensions are flattened prior to comparison. For example, a stereo input with shape (2, d, n) is automatically reshaped to (2 * d, n).

data_refnp.ndarray [shape=(…, d, n_ref)]

A feature matrix for the reference sequence If the data has more than two dimensions (e.g., for multi-channel inputs), the leading dimensions are flattened prior to comparison. For example, a stereo input with shape (2, d, n_ref) is automatically reshaped to (2 * d, n_ref).

kint > 0 [scalar] or None

the number of nearest-neighbors for each sample

Default: k = 2 * ceil(sqrt(n_ref)), or k = 2 if n_ref <= 3

metricstr

Distance metric to use for nearest-neighbor calculation.

See sklearn.neighbors.NearestNeighbors for details.

sparsebool [scalar]

if False, returns a dense type (ndarray) if True, returns a sparse type (scipy.sparse.csc_matrix)

modestr, {‘connectivity’, ‘distance’, ‘affinity’}

If ‘connectivity’, a binary connectivity matrix is produced.

If ‘distance’, then a non-zero entry contains the distance between points.

If ‘affinity’, then non-zero entries are mapped to exp( - distance(i, j) / bandwidth) where bandwidth is as specified below.

bandwidthNone, float > 0, ndarray, or str

str options include {'med_k_scalar', 'mean_k', 'gmean_k', 'mean_k_avg', 'gmean_k_avg', 'mean_k_avg_and_pair'}

If ndarray is supplied, use ndarray as bandwidth for each i,j pair.

If using mode='affinity', this can be used to set the bandwidth on the affinity kernel.

If no value is provided or None, default to 'med_k_scalar'.

If bandwidth='med_k_scalar', bandwidth is set automatically to the median distance to the k’th nearest neighbor of each data[:, i].

If bandwidth='mean_k', bandwidth is estimated for each sample-pair (i, j) by taking the arithmetic mean between distances to the k-th nearest neighbor for sample i and sample j.

If bandwidth='gmean_k', bandwidth is estimated for each sample-pair (i, j) by taking the geometric mean between distances to the k-th nearest neighbor for sample i and j [1].

If bandwidth='mean_k_avg', bandwidth is estimated for each sample-pair (i, j) by taking the arithmetic mean between the average distances to the first k-th nearest neighbors for sample i and sample j. This is similar to the approach in Wang et al. (2014) [2] but does not include the distance between i and j.

If bandwidth='gmean_k_avg', bandwidth is estimated for each sample-pair (i, j) by taking the geometric mean between the average distances to the first k-th nearest neighbors for sample i and sample j.

If bandwidth='mean_k_avg_and_pair', bandwidth is estimated for each sample-pair (i, j) by taking the arithmetic mean between three terms: the average distances to the first k-th nearest neighbors for sample i and sample j respectively, as well as the distance between i and j. This is similar to the approach in Wang et al. (2014). [2]

[1]

Zelnik-Manor, Lihi, and Pietro Perona. (2004). “Self-tuning spectral clustering.” Advances in neural information processing systems 17.

[2] (1,2)

Wang, Bo, et al. (2014). “Similarity network fusion for aggregating data types on a genomic scale.” Nat Methods 11, 333–337. https://doi.org/10.1038/nmeth.2810

fullbool

If using mode ='affinity' or mode='distance', this option can be used to compute the full affinity or distance matrix as opposed a sparse matrix with only none-zero terms for the first k-neighbors of each sample. This option has no effect when using mode='connectivity'.

When using mode='distance', setting full=True will ignore k and width. When using mode='affinity', setting full=True will use k exclusively for bandwidth estimation, and ignore width.

Returns:

xsimnp.ndarray or scipy.sparse.csc_matrix, [shape=(n_ref, n)]

Cross-similarity matrix

See also

recurrence_matrix

recurrence_to_lag

librosa.feature.stack_memory

sklearn.neighbors.NearestNeighbors

scipy.spatial.distance.cdist

Notes

This function caches at level 30.

Examples

Find nearest neighbors in CQT space between two sequences

>>> hop_length = 1024
>>> y_ref, sr = librosa.load(librosa.ex('pistachio'))
>>> y_comp, sr = librosa.load(librosa.ex('pistachio'), offset=10)
>>> chroma_ref = librosa.feature.chroma_cqt(y=y_ref, sr=sr, hop_length=hop_length)
>>> chroma_comp = librosa.feature.chroma_cqt(y=y_comp, sr=sr, hop_length=hop_length)
>>> # Use time-delay embedding to get a cleaner recurrence matrix
>>> x_ref = librosa.feature.stack_memory(chroma_ref, n_steps=10, delay=3)
>>> x_comp = librosa.feature.stack_memory(chroma_comp, n_steps=10, delay=3)
>>> xsim = librosa.segment.cross_similarity(x_comp, x_ref)

Or fix the number of nearest neighbors to 5

>>> xsim = librosa.segment.cross_similarity(x_comp, x_ref, k=5)

Use cosine similarity instead of Euclidean distance

>>> xsim = librosa.segment.cross_similarity(x_comp, x_ref, metric='cosine')

Use an affinity matrix instead of binary connectivity

>>> xsim_aff = librosa.segment.cross_similarity(x_comp, x_ref, metric='cosine', mode='affinity')

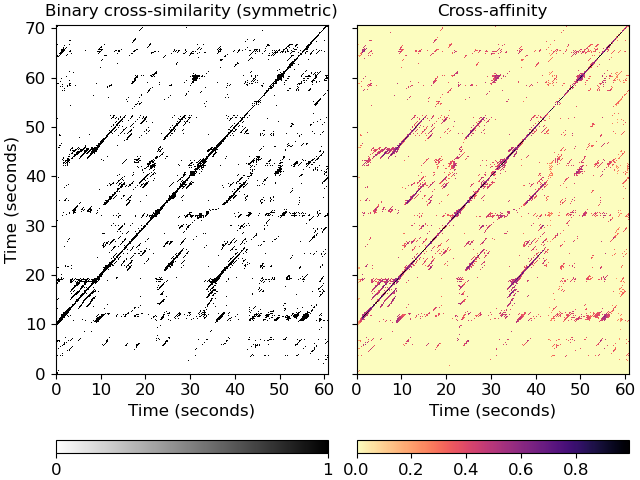
Plot the feature and recurrence matrices

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(ncols=2, sharex=True, sharey=True)
>>> imgsim = librosa.display.specshow(xsim, x_axis='s', y_axis='s',
...                          hop_length=hop_length, ax=ax[0])
>>> ax[0].set(title='Binary cross-similarity (symmetric)')
>>> imgaff = librosa.display.specshow(xsim_aff, x_axis='s', y_axis='s',
...                          cmap='magma_r', hop_length=hop_length, ax=ax[1])
>>> ax[1].set(title='Cross-affinity')
>>> ax[1].label_outer()
>>> fig.colorbar(imgsim, ax=ax[0], orientation='horizontal', ticks=[0, 1])
>>> fig.colorbar(imgaff, ax=ax[1], orientation='horizontal')