Caution

You're reading an old version of this documentation. If you want up-to-date information, please have a look at 0.10.2.

librosa.fmt

librosa.fmt(y, t_min=0.5, n_fmt=None, kind='cubic', beta=0.5, over_sample=1, axis=-1)[source]

The fast Mellin transform (FMT)

The Mellin of a signal y is performed by interpolating y on an exponential time axis, applying a polynomial window, and then taking the discrete Fourier transform.

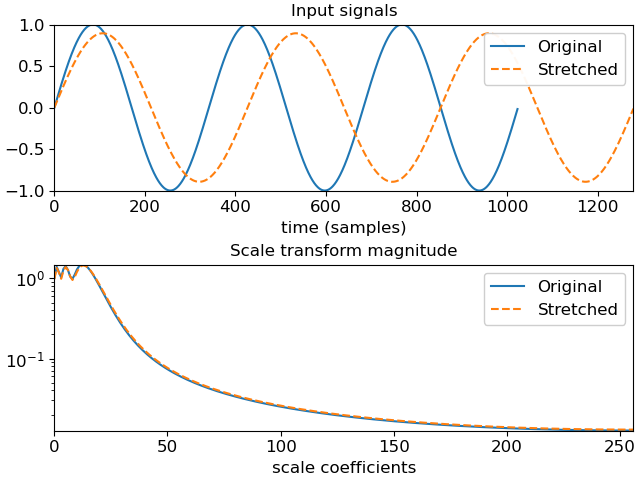
When the Mellin parameter (beta) is 1/2, it is also known as the scale transform. [1] The scale transform can be useful for audio analysis because its magnitude is invariant to scaling of the domain (e.g., time stretching or compression). This is analogous to the magnitude of the Fourier transform being invariant to shifts in the input domain.

Parameters:

ynp.ndarray, real-valued

The input signal(s). Can be multidimensional. The target axis must contain at least 3 samples.

t_minfloat > 0

The minimum time spacing (in samples). This value should generally be less than 1 to preserve as much information as possible.

n_fmtint > 2 or None

The number of scale transform bins to use. If None, then n_bins = over_sample * ceil(n * log((n-1)/t_min)) is taken, where n = y.shape[axis]

kindstr

The type of interpolation to use when re-sampling the input. See scipy.interpolate.interp1d for possible values.

Note that the default is to use high-precision (cubic) interpolation. This can be slow in practice; if speed is preferred over accuracy, then consider using kind='linear'.

betafloat

The Mellin parameter. beta=0.5 provides the scale transform.

over_samplefloat >= 1

Over-sampling factor for exponential resampling.

axisint

The axis along which to transform y

Returns:

x_scalenp.ndarray [dtype=complex]: The scale transform of y along the axis dimension.

Raises:

ParameterError: if n_fmt < 2 or t_min <= 0 or if y is not finite or if y.shape[axis] < 3.

Notes

This function caches at level 30.

Examples

>>> # Generate a signal and time-stretch it (with energy normalization)
>>> scale = 1.25
>>> freq = 3.0
>>> x1 = np.linspace(0, 1, num=1024, endpoint=False)
>>> x2 = np.linspace(0, 1, num=int(scale * len(x1)), endpoint=False)
>>> y1 = np.sin(2 * np.pi * freq * x1)
>>> y2 = np.sin(2 * np.pi * freq * x2) / np.sqrt(scale)
>>> # Verify that the two signals have the same energy
>>> np.sum(np.abs(y1)**2), np.sum(np.abs(y2)**2)
    (255.99999999999997, 255.99999999999969)
>>> scale1 = librosa.fmt(y1, n_fmt=512)
>>> scale2 = librosa.fmt(y2, n_fmt=512)

>>> # And plot the results
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(nrows=2)
>>> ax[0].plot(y1, label='Original')
>>> ax[0].plot(y2, linestyle='--', label='Stretched')
>>> ax[0].set(xlabel='time (samples)', title='Input signals')
>>> ax[0].legend()
>>> ax[1].semilogy(np.abs(scale1), label='Original')
>>> ax[1].semilogy(np.abs(scale2), linestyle='--', label='Stretched')
>>> ax[1].set(xlabel='scale coefficients', title='Scale transform magnitude')
>>> ax[1].legend()

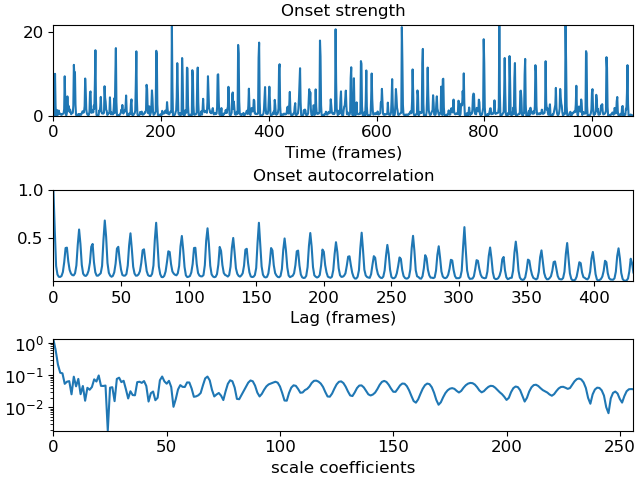
>>> # Plot the scale transform of an onset strength autocorrelation
>>> y, sr = librosa.load(librosa.ex('choice'))
>>> odf = librosa.onset.onset_strength(y=y, sr=sr)
>>> # Auto-correlate with up to 10 seconds lag
>>> odf_ac = librosa.autocorrelate(odf, max_size=10 * sr // 512)
>>> # Normalize
>>> odf_ac = librosa.util.normalize(odf_ac, norm=np.inf)
>>> # Compute the scale transform
>>> odf_ac_scale = librosa.fmt(librosa.util.normalize(odf_ac), n_fmt=512)
>>> # Plot the results
>>> fig, ax = plt.subplots(nrows=3)
>>> ax[0].plot(odf, label='Onset strength')
>>> ax[0].set(xlabel='Time (frames)', title='Onset strength')
>>> ax[1].plot(odf_ac, label='Onset autocorrelation')
>>> ax[1].set(xlabel='Lag (frames)', title='Onset autocorrelation')
>>> ax[2].semilogy(np.abs(odf_ac_scale), label='Scale transform magnitude')
>>> ax[2].set(xlabel='scale coefficients')