Caution

You're reading an old version of this documentation. If you want up-to-date information, please have a look at 0.10.2.

librosa.segment.cross_similarity

librosa.segment.cross_similarity(data, data_ref, *, k=None, metric='euclidean', sparse=False, mode='connectivity', bandwidth=None)

Compute cross-similarity from one data sequence to a reference sequence.

The output is a matrix xsim, where xsim[i, j] is non-zero if data_ref[..., i] is a k-nearest neighbor of data[..., j].

Parameters:

datanp.ndarray [shape=(…, d, n)]

A feature matrix for the comparison sequence. If the data has more than two dimensions (e.g., for multi-channel inputs), the leading dimensions are flattened prior to comparison. For example, a stereo input with shape (2, d, n) is automatically reshaped to (2 * d, n).

data_refnp.ndarray [shape=(…, d, n_ref)]

A feature matrix for the reference sequence If the data has more than two dimensions (e.g., for multi-channel inputs), the leading dimensions are flattened prior to comparison. For example, a stereo input with shape (2, d, n_ref) is automatically reshaped to (2 * d, n_ref).

kint > 0 [scalar] or None

the number of nearest-neighbors for each sample

Default: k = 2 * ceil(sqrt(n_ref)), or k = 2 if n_ref <= 3

metricstr

Distance metric to use for nearest-neighbor calculation.

See sklearn.neighbors.NearestNeighbors for details.

sparsebool [scalar]

if False, returns a dense type (ndarray) if True, returns a sparse type (scipy.sparse.csc_matrix)

modestr, {‘connectivity’, ‘distance’, ‘affinity’}

If ‘connectivity’, a binary connectivity matrix is produced.

If ‘distance’, then a non-zero entry contains the distance between points.

If ‘affinity’, then non-zero entries are mapped to exp( - distance(i, j) / bandwidth) where bandwidth is as specified below.

bandwidthNone or float > 0

If using mode='affinity', this can be used to set the bandwidth on the affinity kernel.

If no value is provided, it is set automatically to the median distance to the k’th nearest neighbor of each data[:, i].

Returns:

xsimnp.ndarray or scipy.sparse.csc_matrix, [shape=(n_ref, n)]

Cross-similarity matrix

See also

recurrence_matrix

recurrence_to_lag

librosa.feature.stack_memory

sklearn.neighbors.NearestNeighbors

scipy.spatial.distance.cdist

Notes

This function caches at level 30.

Examples

Find nearest neighbors in CQT space between two sequences

>>> hop_length = 1024
>>> y_ref, sr = librosa.load(librosa.ex('pistachio'))
>>> y_comp, sr = librosa.load(librosa.ex('pistachio'), offset=10)
>>> chroma_ref = librosa.feature.chroma_cqt(y=y_ref, sr=sr, hop_length=hop_length)
>>> chroma_comp = librosa.feature.chroma_cqt(y=y_comp, sr=sr, hop_length=hop_length)
>>> # Use time-delay embedding to get a cleaner recurrence matrix
>>> x_ref = librosa.feature.stack_memory(chroma_ref, n_steps=10, delay=3)
>>> x_comp = librosa.feature.stack_memory(chroma_comp, n_steps=10, delay=3)
>>> xsim = librosa.segment.cross_similarity(x_comp, x_ref)

Or fix the number of nearest neighbors to 5

>>> xsim = librosa.segment.cross_similarity(x_comp, x_ref, k=5)

Use cosine similarity instead of Euclidean distance

>>> xsim = librosa.segment.cross_similarity(x_comp, x_ref, metric='cosine')

Use an affinity matrix instead of binary connectivity

>>> xsim_aff = librosa.segment.cross_similarity(x_comp, x_ref, metric='cosine', mode='affinity')

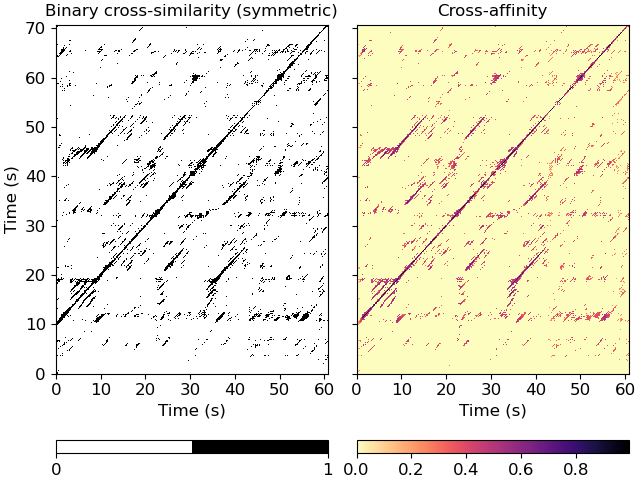
Plot the feature and recurrence matrices

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(ncols=2, sharex=True, sharey=True)
>>> imgsim = librosa.display.specshow(xsim, x_axis='s', y_axis='s',
...                          hop_length=hop_length, ax=ax[0])
>>> ax[0].set(title='Binary cross-similarity (symmetric)')
>>> imgaff = librosa.display.specshow(xsim_aff, x_axis='s', y_axis='s',
...                          cmap='magma_r', hop_length=hop_length, ax=ax[1])
>>> ax[1].set(title='Cross-affinity')
>>> ax[1].label_outer()
>>> fig.colorbar(imgsim, ax=ax[0], orientation='horizontal', ticks=[0, 1])
>>> fig.colorbar(imgaff, ax=ax[1], orientation='horizontal')