Caution

You're reading an old version of this documentation. If you want up-to-date information, please have a look at 0.9.1.

librosa.feature.delta

librosa.feature.delta(data, width=9, order=1, axis=- 1, mode='interp', **kwargs)

Compute delta features: local estimate of the derivative of the input data along the selected axis.

Delta features are computed Savitsky-Golay filtering.

Parameters

datanp.ndarray

the input data matrix (eg, spectrogram)

widthint, positive, odd [scalar]

Number of frames over which to compute the delta features. Cannot exceed the length of data along the specified axis. If mode=’interp’, then width must be at least data.shape[axis].

orderint > 0 [scalar]

the order of the difference operator. 1 for first derivative, 2 for second, etc.

axisint [scalar]

the axis along which to compute deltas. Default is -1 (columns).

modestr, {‘interp’, ‘nearest’, ‘mirror’, ‘constant’, ‘wrap’}

Padding mode for estimating differences at the boundaries.

kwargsadditional keyword arguments

See scipy.signal.savgol_filter

Returns

delta_datanp.ndarray [shape=(d, t)]

delta matrix of data at specified order

See also

scipy.signal.savgol_filter

Notes

This function caches at level 40.

Examples

Compute MFCC deltas, delta-deltas

>>> y, sr = librosa.load(librosa.util.example_audio_file())
>>> mfcc = librosa.feature.mfcc(y=y, sr=sr)
>>> mfcc_delta = librosa.feature.delta(mfcc)
>>> mfcc_delta
array([[  1.666e+01,   1.666e+01, ...,   1.869e-15,   1.869e-15],
       [  1.784e+01,   1.784e+01, ...,   6.085e-31,   6.085e-31],
       ...,
       [  7.262e-01,   7.262e-01, ...,   9.259e-31,   9.259e-31],
       [  6.578e-01,   6.578e-01, ...,   7.597e-31,   7.597e-31]])

>>> mfcc_delta2 = librosa.feature.delta(mfcc, order=2)
>>> mfcc_delta2
array([[ -1.703e+01,  -1.703e+01, ...,   3.834e-14,   3.834e-14],
       [ -1.108e+01,  -1.108e+01, ...,  -1.068e-30,  -1.068e-30],
       ...,
       [  4.075e-01,   4.075e-01, ...,  -1.565e-30,  -1.565e-30],
       [  1.676e-01,   1.676e-01, ...,  -2.104e-30,  -2.104e-30]])

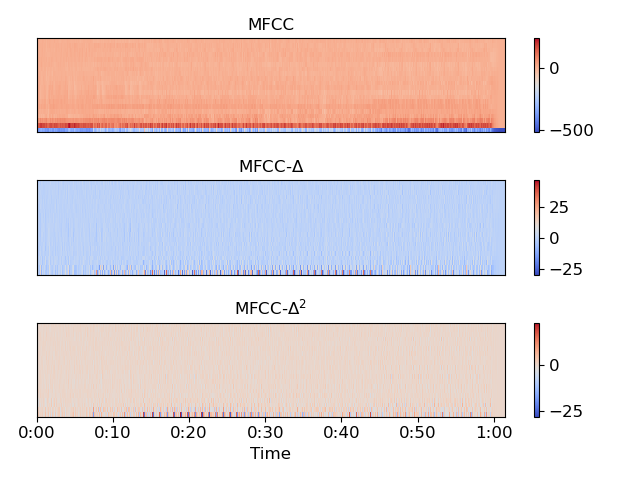
>>> import matplotlib.pyplot as plt
>>> plt.subplot(3, 1, 1)
>>> librosa.display.specshow(mfcc)
>>> plt.title('MFCC')
>>> plt.colorbar()
>>> plt.subplot(3, 1, 2)
>>> librosa.display.specshow(mfcc_delta)
>>> plt.title(r'MFCC-$\Delta$')
>>> plt.colorbar()
>>> plt.subplot(3, 1, 3)
>>> librosa.display.specshow(mfcc_delta2, x_axis='time')
>>> plt.title(r'MFCC-$\Delta^2$')
>>> plt.colorbar()
>>> plt.tight_layout()
>>> plt.show()