Caution

You're reading an old version of this documentation. If you want up-to-date information, please have a look at 0.9.1.

librosa.segment.recurrence_matrix

librosa.segment.recurrence_matrix(data, k=None, width=1, metric='euclidean', sym=False, sparse=False, mode='connectivity', bandwidth=None, self=False, axis=- 1)

Compute a recurrence matrix from a data matrix.

rec[i, j] is non-zero if data[:, i] is one of data[:, j]’s k-nearest-neighbors and |i - j| >= width

The specific value of rec[i, j] can have several forms, governed by the mode parameter below:

• Connectivity: rec[i, j] = 1 or 0 indicates that frames i and j are repetitions

• Affinity: rec[i, j] > 0 measures how similar frames i and j are. This is also known as a (sparse) self-similarity matrix.

• Distance: rec[i, j] > 0 measures how distant frames i and j are. This is also known as a (sparse) self-distance matrix.

The general term recurrence matrix can refer to any of the three forms above.

Parameters

datanp.ndarray

A feature matrix

kint > 0 [scalar] or None

the number of nearest-neighbors for each sample

Default: k = 2 * ceil(sqrt(t - 2 * width + 1)), or k = 2 if t <= 2 * width + 1

widthint >= 1 [scalar]

only link neighbors (data[:, i], data[:, j]) if |i - j| >= width

width cannot exceed the length of the data.

metricstr

Distance metric to use for nearest-neighbor calculation.

See sklearn.neighbors.NearestNeighbors for details.

symbool [scalar]

set sym=True to only link mutual nearest-neighbors

sparsebool [scalar]

if False, returns a dense type (ndarray) if True, returns a sparse type (scipy.sparse.csc_matrix)

modestr, {‘connectivity’, ‘distance’, ‘affinity’}

If ‘connectivity’, a binary connectivity matrix is produced.

If ‘distance’, then a non-zero entry contains the distance between points.

If ‘affinity’, then non-zero entries are mapped to exp( - distance(i, j) / bandwidth) where bandwidth is as specified below.

bandwidthNone or float > 0

If using mode='affinity', this can be used to set the bandwidth on the affinity kernel.

If no value is provided, it is set automatically to the median distance between furthest nearest neighbors.

selfbool

If True, then the main diagonal is populated with self-links: 0 if mode='distance', and 1 otherwise.

If False, the main diagonal is left empty.

axisint

The axis along which to compute recurrence. By default, the last index (-1) is taken.

Returns

recnp.ndarray or scipy.sparse.csc_matrix, [shape=(t, t)]

Recurrence matrix

See also

sklearn.neighbors.NearestNeighbors

scipy.spatial.distance.cdist

librosa.feature.stack_memory

recurrence_to_lag

Notes

This function caches at level 30.

Examples

Find nearest neighbors in MFCC space

>>> y, sr = librosa.load(librosa.util.example_audio_file())
>>> hop_length = 1024
>>> mfcc = librosa.feature.mfcc(y=y, sr=sr, hop_length=hop_length)
>>> R = librosa.segment.recurrence_matrix(mfcc)

Or fix the number of nearest neighbors to 5

>>> R = librosa.segment.recurrence_matrix(mfcc, k=5)

Suppress neighbors within +- 7 frames

>>> R = librosa.segment.recurrence_matrix(mfcc, width=7)

Use cosine similarity instead of Euclidean distance

>>> R = librosa.segment.recurrence_matrix(mfcc, metric='cosine')

Require mutual nearest neighbors

>>> R = librosa.segment.recurrence_matrix(mfcc, sym=True)

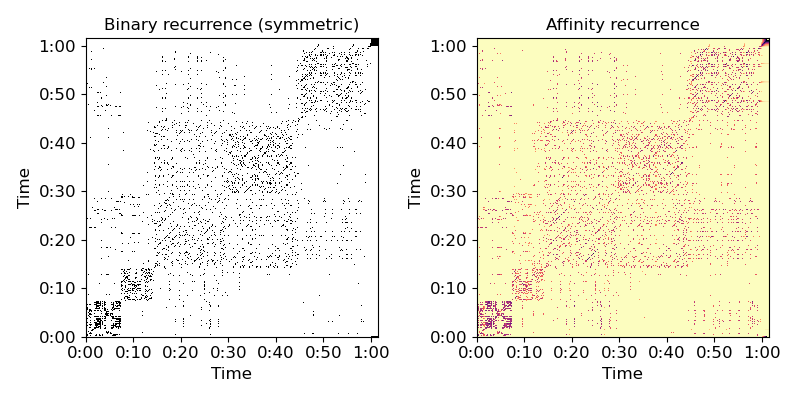
Use an affinity matrix instead of binary connectivity

>>> R_aff = librosa.segment.recurrence_matrix(mfcc, mode='affinity')

Plot the feature and recurrence matrices

>>> import matplotlib.pyplot as plt
>>> plt.figure(figsize=(8, 4))
>>> plt.subplot(1, 2, 1)
>>> librosa.display.specshow(R, x_axis='time', y_axis='time', hop_length=hop_length)
>>> plt.title('Binary recurrence (symmetric)')
>>> plt.subplot(1, 2, 2)
>>> librosa.display.specshow(R_aff, x_axis='time', y_axis='time',
...                          hop_length=hop_length, cmap='magma_r')
>>> plt.title('Affinity recurrence')
>>> plt.tight_layout()
>>> plt.show()