librosa.lpc
- librosa.lpc(y, *, order, axis=-1)[source]
Linear Prediction Coefficients via Burg’s method
This function applies Burg’s method to estimate coefficients of a linear filter on
yof orderorder. Burg’s method is an extension to the Yule-Walker approach, which are both sometimes referred to as LPC parameter estimation by autocorrelation.It follows the description and implementation approach described in the introduction by Marple. [1] N.B. This paper describes a different method, which is not implemented here, but has been chosen for its clear explanation of Burg’s technique in its introduction.
- Parameters:
- ynp.ndarray [shape=(…, n)]
Time series to fit. Multi-channel is supported..
- orderint > 0
Order of the linear filter
- axisint
Axis along which to compute the coefficients
- Returns:
- anp.ndarray [shape=(…, order + 1)]
LP prediction error coefficients, i.e. filter denominator polynomial. Note that the length along the specified
axiswill beorder+1.
- Raises:
- ParameterError
If
yis not valid audio as perlibrosa.util.valid_audioIf
order < 1or not integer
- FloatingPointError
If
yis ill-conditioned
See also
Examples
Compute LP coefficients of y at order 16 on entire series
>>> y, sr = librosa.load(librosa.ex('libri1')) >>> librosa.lpc(y, order=16)
Compute LP coefficients, and plot LP estimate of original series
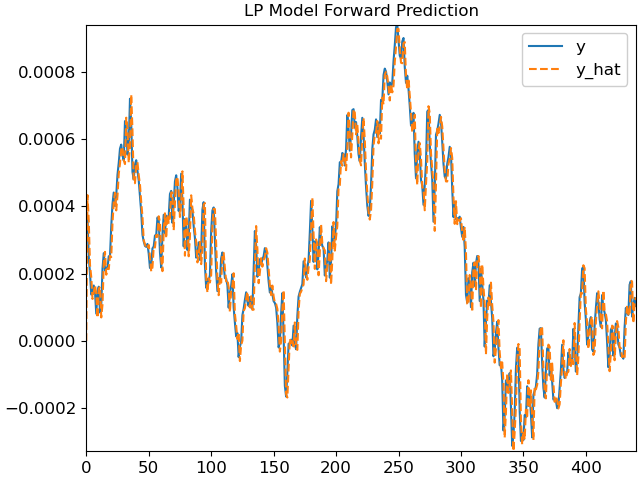
>>> import matplotlib.pyplot as plt >>> import scipy >>> y, sr = librosa.load(librosa.ex('libri1'), duration=0.020) >>> a = librosa.lpc(y, order=2) >>> b = np.hstack([[0], -1 * a[1:]]) >>> y_hat = scipy.signal.lfilter(b, [1], y) >>> fig, ax = plt.subplots() >>> ax.plot(y) >>> ax.plot(y_hat, linestyle='--') >>> ax.legend(['y', 'y_hat']) >>> ax.set_title('LP Model Forward Prediction')