Caution

You're reading the documentation for a development version. For the latest released version, please have a look at 0.10.2.

librosa.filters.mel

librosa.filters.mel(*, sr, n_fft, n_mels=128, fmin=0.0, fmax=None, htk=False, norm='slaney', dtype=<class 'numpy.float32'>)[source]

Create a Mel filter-bank.

This produces a linear transformation matrix to project FFT bins onto Mel-frequency bins.

Parameters:

srnumber > 0 [scalar]

sampling rate of the incoming signal

n_fftint > 0 [scalar]

number of FFT components

n_melsint > 0 [scalar]

number of Mel bands to generate

fminfloat >= 0 [scalar]

lowest frequency (in Hz)

fmaxfloat >= 0 [scalar]

highest frequency (in Hz). If None, use fmax = sr / 2.0

htkbool [scalar]

use HTK formula instead of Slaney

norm{None, ‘slaney’, or number} [scalar]

If ‘slaney’, divide the triangular mel weights by the width of the mel band (area normalization).

If numeric, use librosa.util.normalize to normalize each filter by to unit l_p norm. See librosa.util.normalize for a full description of supported norm values (including +-np.inf).

Otherwise, leave all the triangles aiming for a peak value of 1.0

dtypenp.dtype

The data type of the output basis. By default, uses 32-bit (single-precision) floating point.

Returns:

Mnp.ndarray [shape=(n_mels, 1 + n_fft/2)]: Mel transform matrix

See also

librosa.util.normalize

Notes

This function caches at level 10.

Examples

>>> melfb = librosa.filters.mel(sr=22050, n_fft=2048)
>>> melfb
array([[ 0.   ,  0.016, ...,  0.   ,  0.   ],
       [ 0.   ,  0.   , ...,  0.   ,  0.   ],
       ...,
       [ 0.   ,  0.   , ...,  0.   ,  0.   ],
       [ 0.   ,  0.   , ...,  0.   ,  0.   ]])

Clip the maximum frequency to 8KHz

>>> librosa.filters.mel(sr=22050, n_fft=2048, fmax=8000)
array([[ 0.  ,  0.02, ...,  0.  ,  0.  ],
       [ 0.  ,  0.  , ...,  0.  ,  0.  ],
       ...,
       [ 0.  ,  0.  , ...,  0.  ,  0.  ],
       [ 0.  ,  0.  , ...,  0.  ,  0.  ]])

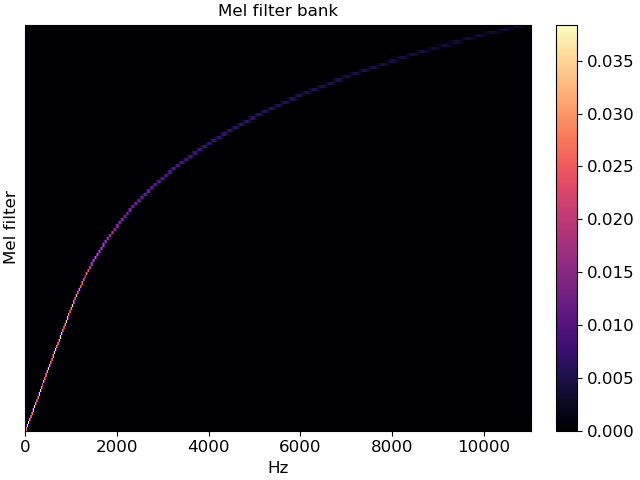
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> img = librosa.display.specshow(melfb, x_axis='linear', ax=ax)
>>> ax.set(ylabel='Mel filter', title='Mel filter bank')
>>> fig.colorbar(img, ax=ax)