Caution

You're reading the documentation for a development version. For the latest released version, please have a look at 0.10.2.

librosa.feature.melspectrogram

librosa.feature.melspectrogram(*, y=None, sr=22050, S=None, n_fft=2048, hop_length=512, win_length=None, window='hann', center=True, pad_mode='constant', power=2.0, **kwargs)

Compute a mel-scaled spectrogram.

If a spectrogram input S is provided, then it is mapped directly onto the mel basis by mel_f.dot(S).

If a time-series input y, sr is provided, then its magnitude spectrogram S is first computed, and then mapped onto the mel scale by mel_f.dot(S**power).

By default, power=2 operates on a power spectrum.

Parameters:

ynp.ndarray [shape=(…, n)] or None

audio time-series. Multi-channel is supported.

srnumber > 0 [scalar]

sampling rate of y

Snp.ndarray [shape=(…, d, t)]

spectrogram

n_fftint > 0 [scalar]

length of the FFT window

hop_lengthint > 0 [scalar]

number of samples between successive frames. See librosa.stft

win_lengthint <= n_fft [scalar]

Each frame of audio is windowed by window(). The window will be of length win_length and then padded with zeros to match n_fft. If unspecified, defaults to win_length = n_fft.

windowstring, tuple, number, function, or np.ndarray [shape=(n_fft,)]

• a window specification (string, tuple, or number); see scipy.signal.get_window

• a window function, such as scipy.signal.windows.hann

• a vector or array of length n_fft

centerboolean

• If True, the signal y is padded so that frame t is centered at y[t * hop_length].

• If False, then frame t begins at y[t * hop_length]

pad_modestring

If center=True, the padding mode to use at the edges of the signal. By default, STFT uses zero padding.

powerfloat > 0 [scalar]

Exponent for the magnitude melspectrogram. e.g., 1 for energy, 2 for power, etc.

**kwargsadditional keyword arguments for Mel filter bank parameters

n_melsint > 0 [scalar]

number of Mel bands to generate

fminfloat >= 0 [scalar]

lowest frequency (in Hz)

fmaxfloat >= 0 [scalar]

highest frequency (in Hz). If None, use fmax = sr / 2.0

htkbool [scalar]

use HTK formula instead of Slaney

norm{None, ‘slaney’, or number} [scalar]

If ‘slaney’, divide the triangular mel weights by the width of the mel band (area normalization). If numeric, use librosa.util.normalize to normalize each filter by to unit l_p norm. See librosa.util.normalize for a full description of supported norm values (including +-np.inf). Otherwise, leave all the triangles aiming for a peak value of 1.0

dtypenp.dtype

The data type of the output basis. By default, uses 32-bit (single-precision) floating point.

Returns:

Snp.ndarray [shape=(…, n_mels, t)]

Mel spectrogram

See also

librosa.filters.mel

Mel filter bank construction

librosa.stft

Short-time Fourier Transform

Examples

>>> y, sr = librosa.load(librosa.ex('trumpet'))
>>> librosa.feature.melspectrogram(y=y, sr=sr)
array([[3.837e-06, 1.451e-06, ..., 8.352e-14, 1.296e-11],
       [2.213e-05, 7.866e-06, ..., 8.532e-14, 1.329e-11],
       ...,
       [1.115e-05, 5.192e-06, ..., 3.675e-08, 2.470e-08],
       [6.473e-07, 4.402e-07, ..., 1.794e-08, 2.908e-08]],
      dtype=float32)

Using a pre-computed power spectrogram would give the same result:

>>> D = np.abs(librosa.stft(y))**2
>>> S = librosa.feature.melspectrogram(S=D, sr=sr)

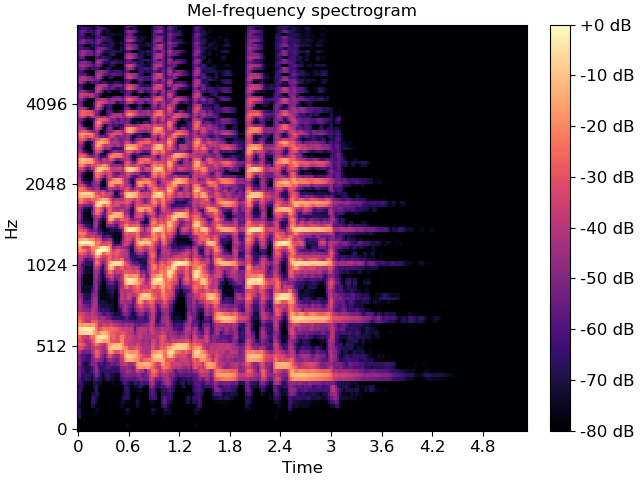
Display of mel-frequency spectrogram coefficients, with custom arguments for mel filterbank construction (default is fmax=sr/2):

>>> # Passing through arguments to the Mel filters
>>> S = librosa.feature.melspectrogram(y=y, sr=sr, n_mels=128,
...                                     fmax=8000)

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> S_dB = librosa.power_to_db(S, ref=np.max)
>>> img = librosa.display.specshow(S_dB, x_axis='time',
...                          y_axis='mel', sr=sr,
...                          fmax=8000, ax=ax)
>>> fig.colorbar(img, ax=ax, format='%+2.0f dB')
>>> ax.set(title='Mel-frequency spectrogram')