librosa.feature.spectral_bandwidth

librosa.feature.spectral_bandwidth(*, y=None, sr=22050, S=None, n_fft=2048, hop_length=512, win_length=None, window='hann', center=True, pad_mode='constant', freq=None, centroid=None, norm=True, p=2)[source]

Compute p’th-order spectral bandwidth.

The spectral bandwidth [1] at frame t is computed by:

(sum_k S[k, t] * (freq[k, t] - centroid[t])**p)**(1/p)
Parameters:
ynp.ndarray [shape=(…, n)] or None

audio time series. Multi-channel is supported.

srnumber > 0 [scalar]

audio sampling rate of y

Snp.ndarray [shape=(…, d, t)] or None

(optional) spectrogram magnitude

n_fftint > 0 [scalar]

FFT window size

hop_lengthint > 0 [scalar]

hop length for STFT. See librosa.stft for details.

win_lengthint <= n_fft [scalar]

Each frame of audio is windowed by window(). The window will be of length win_length and then padded with zeros to match n_fft. If unspecified, defaults to win_length = n_fft.

windowstring, tuple, number, function, or np.ndarray [shape=(n_fft,)]
centerboolean

  • If True, the signal y is padded so that frame t is centered at y[t * hop_length].

  • If False, then frame t begins at y[t * hop_length]

pad_modestring

If center=True, the padding mode to use at the edges of the signal. By default, STFT uses zero padding.

freqNone or np.ndarray [shape=(d,) or shape=(…, d, t)]

Center frequencies for spectrogram bins. If None, then FFT bin center frequencies are used. Otherwise, it can be a single array of d center frequencies, or a matrix of center frequencies as constructed by librosa.reassigned_spectrogram

centroidNone or np.ndarray [shape=(…, 1, t)]

pre-computed centroid frequencies

normbool

Normalize per-frame spectral energy (sum to one)

pfloat > 0

Power to raise deviation from spectral centroid.

Returns:
bandwidthnp.ndarray [shape=(…, 1, t)]

frequency bandwidth for each frame

Examples

From time-series input

>>> y, sr = librosa.load(librosa.ex('trumpet'))
>>> spec_bw = librosa.feature.spectral_bandwidth(y=y, sr=sr)
>>> spec_bw
array([[1273.836, 1228.873, ..., 2952.357, 3013.68 ]])

From spectrogram input

>>> S, phase = librosa.magphase(librosa.stft(y=y))
>>> librosa.feature.spectral_bandwidth(S=S)
array([[1273.836, 1228.873, ..., 2952.357, 3013.68 ]])

Using variable bin center frequencies

>>> freqs, times, D = librosa.reassigned_spectrogram(y, fill_nan=True)
>>> librosa.feature.spectral_bandwidth(S=np.abs(D), freq=freqs)
array([[1274.637, 1228.786, ..., 2952.4  , 3013.735]])

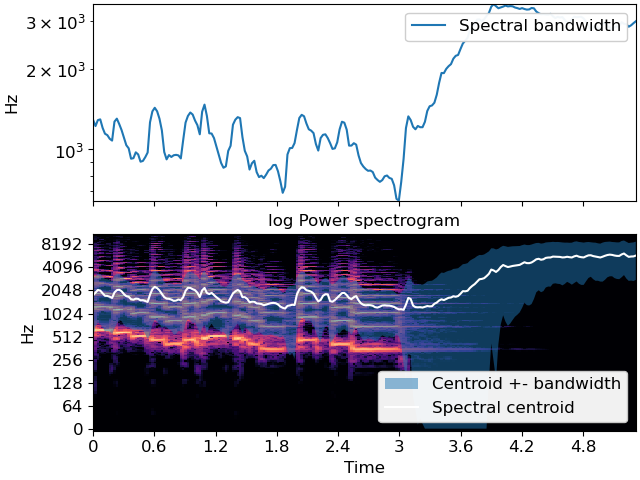
Plot the result

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(nrows=2, sharex=True)
>>> times = librosa.times_like(spec_bw)
>>> centroid = librosa.feature.spectral_centroid(S=S)
>>> ax[0].semilogy(times, spec_bw[0], label='Spectral bandwidth')
>>> ax[0].set(ylabel='Hz', xticks=[], xlim=[times.min(), times.max()])
>>> ax[0].legend()
>>> ax[0].label_outer()
>>> librosa.display.specshow(librosa.amplitude_to_db(S, ref=np.max),
...                          y_axis='log', x_axis='time', ax=ax[1])
>>> ax[1].set(title='log Power spectrogram')
>>> ax[1].fill_between(times, np.maximum(0, centroid[0] - spec_bw[0]),
...                 np.minimum(centroid[0] + spec_bw[0], sr/2),
...                 alpha=0.5, label='Centroid +- bandwidth')
>>> ax[1].plot(times, centroid[0], label='Spectral centroid', color='w')
>>> ax[1].legend(loc='lower right')
../_images/librosa-feature-spectral_bandwidth-1.png